کار با PWM با STM32 | قسمت چهاردهم آموزش STM32 با توابع HAL
در قسمت قبل از سری آموزش STM32 با توابع HAL، در مورد حالتهای Input capture و Output compare در تایمرها، صحبت شد. در این قسمت، جزئیات کار با PWM و نحوه تولید شکل موجهای مختلف بهوسیله آن را بررسی میکنیم.

کنترل شدت روشنایی یک LED به وسیله PWM
همانطور که در قسمتهای اخیر گفتیم، تایمرها کاربردهای زیادی دارند و میتوان آنها را در حالتهای مختلفی تنظیم و استفاده کرد. یکی از حالتهای کاری بسیار پراستفاده تایمرها، PWM یا مدولاسیون پهنای پالس (Pulse-Width Modulation) است. در ادامه، ابتدا این مدولاسیون را معرفی میکنیم و از آن در کنترل میانگین ولتاژ استفاده میکنیم. سپس برای استفاده پیشرفتهتر، به معرفی مفاهیم اولیه تولید سیگنال و فیلتر میپردازیم، سپس چگونگی تولید شکل موجهای مختلف بهوسیله PWM و همچنین نحوه استفاده از PWM بهعنوان یک مبدل دیجیتال به آنالوگ (DAC) را بررسی خواهیم کرد.
Pulse-width modulation
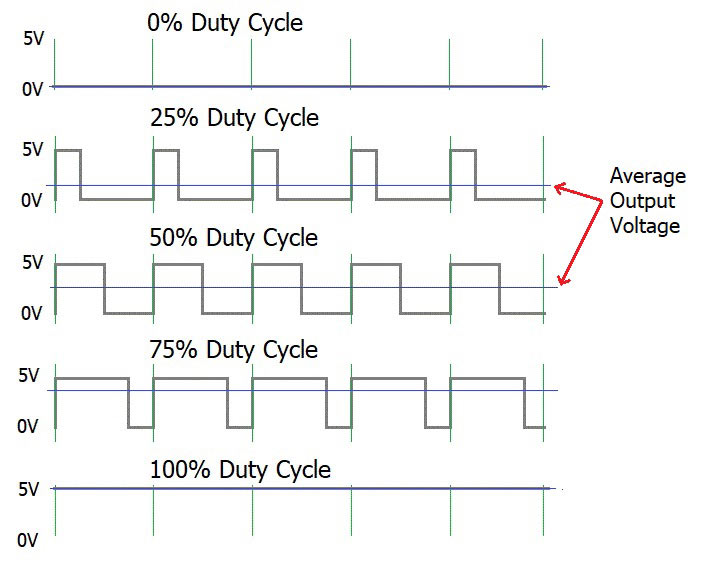
Pulse-width modulation.
همانطور که در شکل بالا مشخص است، بهوسیله PWM میتوانیم از طریق کنترل Duty Cycle یا زمان on بودن و off بودن موج مربعی، ولتاژ متوسط خروجی را کنترل کنیم. این عمل کاربردهای بسیار زیادی دارد که ازجمله آنها میتوان به کنترل شدت روشنایی، کنترل سرعت موتور و… اشاره کرد. سه پارامتر مهم و اساسی در تنظیم PWM، عبارتاند از فرکانس، Duty Cycle و دقت یا وضوح (Resolution) در ادامه به این نقش هر یک از این پارامترها و نحوه تنظیم آنها میپردازیم.
کنترل Duty Cycle
کلاک تایمر در حالت PWM، توسط منبع کلاک داخلی تأمین میشود. تایمر در این حالت یک شکل موج دیجیتال روی پایه خروجی تولید میکند که سیگنال PWM نام دارد. درواقع نحوه کارکرد تایمر در حالت PWM، بدینصورت است که شمارنده تایمر بهصورت افزایشی شمارش میکند تا زمانی که به مقدار ARR برسد، در این زمان پایه خروجی به منطق High میرود. سپس مقدار شمارنده دائما با مقدار ذخیرهشده در CCR (Capture Compare Register) مقایسه میشود. هنگامیکه این دو مقدار برابر باشند، حالت پایه خروجی معکوس (صفر) میشود و تا پایان دوره شمارش در همین حالت باقی میماند. با تکرار این فرایند یک شکل موج مربعی با فرکانس و Duty Cycle دلخواه تولید خواهد شد. پس میتوان گفت که مقدار Duty Cycle سیگنال PWM، به مقدار CCR وابسته است. این وابستگی در شکل زیر نیز نشان دادهشده است.
 تولید دو سیگنال PWM با Duty Cycleهای متفاوت و فرکانس یکسان توسط دو کانال TIM2.
تولید دو سیگنال PWM با Duty Cycleهای متفاوت و فرکانس یکسان توسط دو کانال TIM2.
همچنین فرمول محاسبه Duty Cycle و رابطه آن با مقدار CCR و ARR بهصورت زیر است:
![]()
فرایند توصیفشده برای عملکرد PWM، یعنی کارکرد آن بهصورت بالا شمار، سادهترین حالت تولید سیگنال PWM است و برای فهم راحتتر موضوع انتخابشده است. با این توصیف، حالت بالا شمار تنها حالت عملکرد PWM نیست و حالتهای دیگری نیز برای PWM، وجود دارد.
فرکانس سیگنال PWM
فرکانس سیگنال PWM به فرکانس کلاک داخلی میکروکنترلر و همچنین مقدار Prescaler و رجیستر ARR در تایمر، وابسته است. وابستگی فرکانس این سیگنال به مقدار ARR، در شکل بالا بهوضوح دیده میشود. سختافزار مربوط به کانالهای مختلف تایمر و همچنین خروجیهای آن را در دو قسمت پیشین بررسی کردیم. با توجه به نکات گفتهشده، میدانیم که امکان تولید سیگنالهای PWM با Duty Cycle متفاوت در کانالهای یک تایمر وجود دارد. اگرچه این سیگنالهای فرکانس یکسان خواهند داشت. علاوه بر این، همه این سیگنالها، مانند شکل نشان دادهشده در بالا، بهصورت همزمان (Sync) خواهند بود.
فرمول محاسبه فرکانس با توجه به مقدارهای فرکانس کلاک داخلی، مقدار ARR و همچنین مقدار Prescaler بهصورت زیر نوشته میشود. در این فرمول، میتوان مقدار مطلوب برای فرکانس سیگنال PWM را جایگذاری کرد و مقدار ARR را بهدست آورد؛
![]()
وضوح سیگنال PWM
پارامتر مهم دیگر سیگنال PWM، وضوح یا Resolution است. درواقع وضوح این سیگنال با تعداد مقادیر قابل انتخاب برای Duty Cycle، تعریف میشود. این پارامتر تعیین میکند که Duty Cycle از صفر تا بیشترین حد خود، چند پله را میتواند طی کند. درنتیجه اندازه هر پله یا تعداد پلههای قابل انتخاب، تعیینکننده دقت یا وضوح تنظیم Duty Cycle هستند.
بنابراین پارامتر موردبحث، در تمامی کاربردها، ازجمله تولید سیگنال صوتی، تنظیم سرعت موتور و همچنین کنترل شدت روشنایی، اهمیت دارد. برای بهدست آوردن این پارامتر، با توجه به فرکانس انتخابشده، یا برعکس، میتوان از فرمول زیر استفاده کرد:
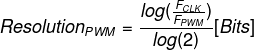
همچنین درصورتیکه بخواهیم وضوح PWM را توسط مقدار ARR استفاده کنیم، میتوانیم از رابطه زیر استفاده کنیم که از همان فرمولهای پیشین، مشتق شده است:
![]()
با توجه به روابط گفتهشده، چند مقدار نمونه برای فرکانس و وضوح PWM، با توجه به فرکانس میکروکنترلر، در جدول زیر آورده شده است:
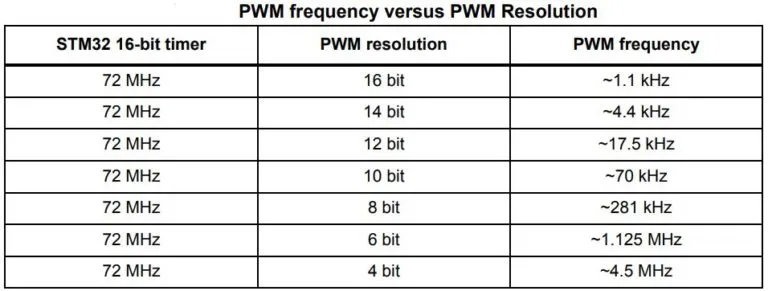
در این مرحله، تا حدی با PWM و نحوه تولید سیگنال بهوسیله آن، آشنا شدیم. در ادامه میخواهیم به ایجاد و توسعه یک پروژه برای تولید سیگنال PWM و کنترل شدت روشنایی LED بهوسیله آن بپردازیم.
ایجاد پروژه کنترل شدت نور LED
مراحل ایجاد پروژه را مثل قبل طی میکنیم و کلاک و دیباگ را تنظیم میکنیم، اما USART را فعال نمیکنیم، زیرا در این پروژه به آن نیازی نداریم. تایمر 1 را بهصورت زیر در حالت PWM تنظیم میکنیم:
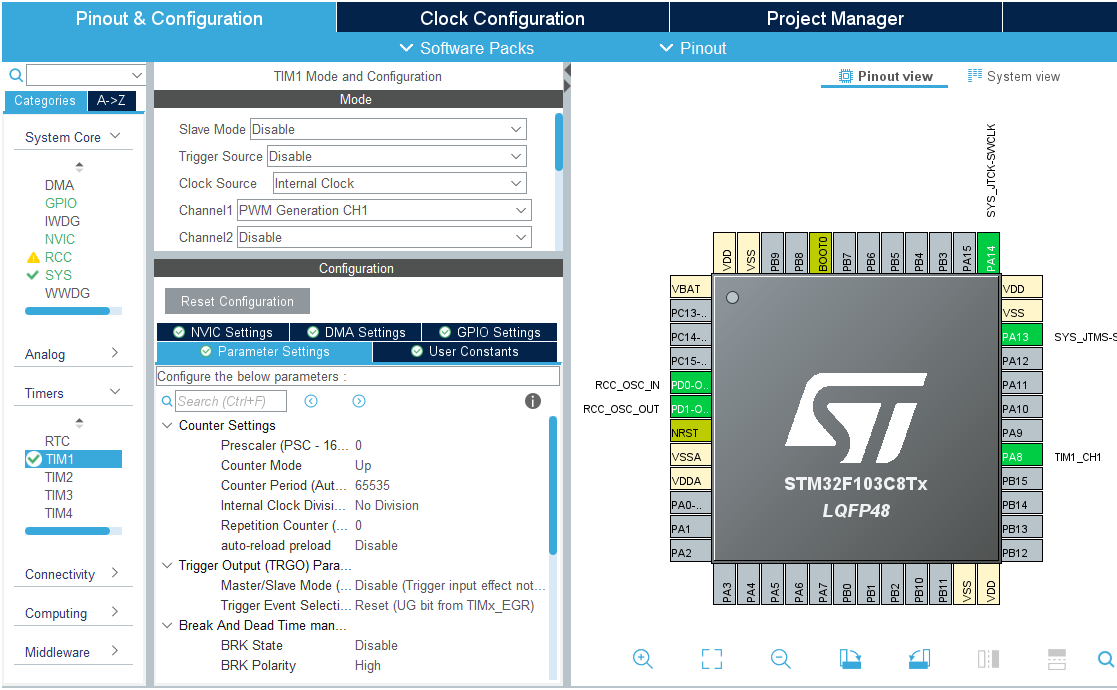
تنظیم TIM1 در حالت PWM.
اکنون میتوانیم به سراغ نوشتن کد برویم.
نوشتن کد پروژه
مانند پروژههای پیشین، قبل از استفاده از تایمر، آن را فعال میکنیم. بدین منظور در بدنه تابع int main و قبل از حلقه while(1)، با نوشتن خط اول کد زیر، این عمل را انجام میدهیم. سپس یک متغیر برای کنترل کردن Duty Cycle و همچنین متغیر max را برای ذخیره مقدار ARR تعریف میکنیم:
|
1 2 3 4 5 6 |
/* USER CODE BEGIN 2 */ HAL_TIM_PWM_Start(&htim1, TIM_CHANNEL_1); uint16_t CH1_DC = 0; uint16_t max = __HAL_TIM_GET_AUTORELOAD(&htim1); /* USER CODE END 2 */ |
سپس بهمنظور روشن و خاموش شدن تدریجی LED، بدنه حلقه while(1) را بهصورت زیر مینویسیم:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
/* USER CODE BEGIN WHILE */ while(CH1_DC < (max * 2 / 3)) { TIM1->CCR1 = CH1_DC; CH1_DC += max/100; HAL_Delay(10); } while(CH1_DC > max / 8) { TIM1->CCR1 = CH1_DC; CH1_DC -= max/100; HAL_Delay(10); } /* USER CODE END WHILE */ |
همانطور که میبینیم، در این کد، ابتدا کوچکتر بودن مقدار Duty Cycle از یک عدد مشخص چک میشود و تا زمان درستی این شرط از طریق افزایش ولتاژ متوسط اعمالی Duty Cycle، و درنتیجه شدت روشنایی LED افزایش مییابد. سپس همین روند بهصورت معکوس طی میشود و شدت روشنایی تا خاموشی کامل LED، کم میگردد. این روند دائما طی میشود.
اکنون یک LED را بهوسیله یک مقاومت حدود 1 کیلو اهمی به پایه PA8 متصل میکنیم. در صورت طی کردن درست تمامی مراحل، میبینیم که پس از کامپایل و دانلود کد روی میکروکنترلر، LED به آهستگی شروع به خاموش و روشن شدن میکند.
تا اینجای کار، چگونگی تولید موج مربعی و کنترل ولتاژ متوسط خروجی بهوسیله PWM را بررسی کردیم. اکنون میخواهیم چگونگی تولید شکل موجهای مختلف توسط PWM را بررسی کنیم.
تولید شکل موجهای مختلف با PWM
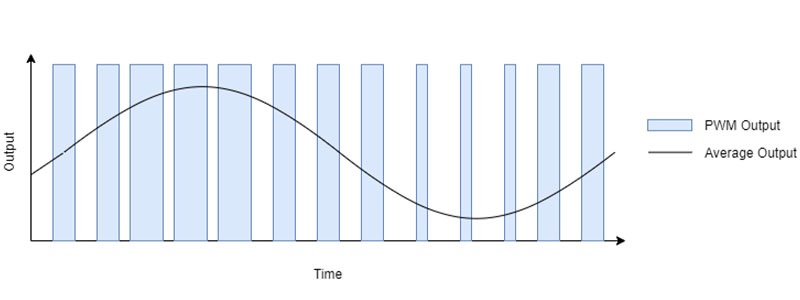
تولید موج سینوسی به وسیله PWM.
مانند کنترل شدت روشنایی، تولید شکل موجهای مختلف نیز بهوسیله کنترل میانگین ولتاژ توسط تغییرات پهنای پالس صورت میگیرد. با این تفاوت که برای ایجاد شکل موجهای غیر از مربعی، میانگین ولتاژ بهصورت متغیر بازمان تنظیم میشود. بهبیاندیگر مقدار میانگین ولتاژ، در هر بازه زمانی و متناسب با شکل موج موردنظر، تغییر خواهد کرد. مثلاً برای یک شکل موج سینونی مثل تصویر بالا با توجه به فرکانسی که برای شکل موج در نظر داریم و همچنین دقتی که برای تولید شکل موج برای ما مطلوب است ولتاژ خروجی را در بازههای مختلف زمانی تنظیم کنیم (مثلاً بهوسیله یک تابع یا یک Look Up Table).
اما قبل از وارد شدن به جزئیات بیشتر در این زمینه، قصد داریم نگاهی به اصول اولیه تولید سیگنال و استفاده از فیلتر بیندازیم.
مقدمهای از سیگنال، طیف فرکانسی و فیلتر
برای اینکه بهتر بتوانیم عملکرد تولید موج بهوسیله PWM را متوجه شویم میخواهیم برخی مفاهیم مرتبط در این زمینه را باهم مرور کنیم. این کار را از اصول اولیه سیگنال شروع میکنیم. به هر سیگنال دلخواهی میتوان از حوزه مختلف نگاه کرد؛ حوزه زمان و حوزه فرکانس. همه نمایش زمانی سیگنالها (مثل شکل موج سینوسی که در بالا دیدیم) را بارها و بارها دیدهایم و با آن آشنایی داریم. نمایش زمانی همان نمودار ولتاژ-زمان یک سیگنال است که تغییرات ولتاژ تابع سیگنال را برحسب زمان نشان میدهد. اما حوزه فرکانس چیست و نمایش سیگنال در این حوزه به چه صورت است؟
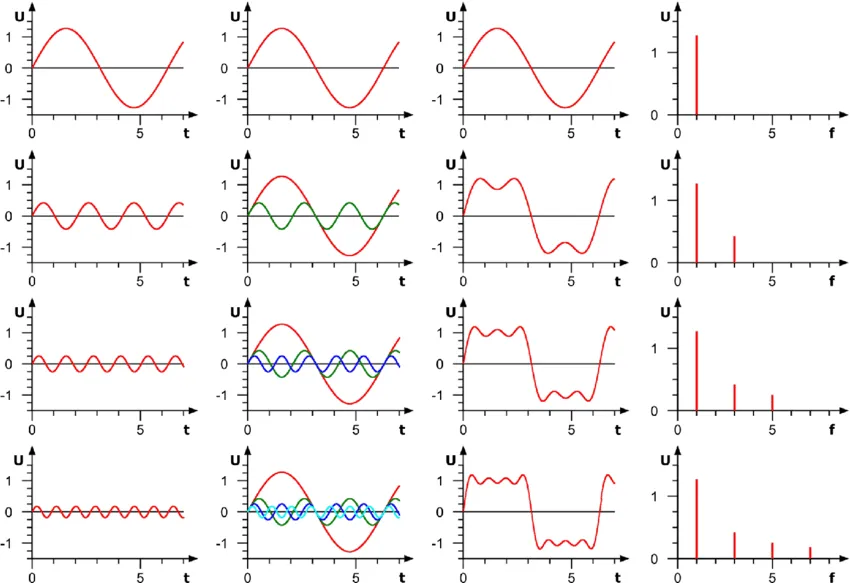
حوزه فرکانس، فضایی است که در آن توابع ریاضی (یا سیگنالها) بر اساس فرکانس بیان میشوند. برای نمایش یک سیگنال در حوزه فرکانس باید از تبدیل فوریه یا FFT کمک گرفت. بدین طریق اجزاء سازنده سیگنال در حوزه فرکانس را خواهیم داشت. به بیان دیگری میتوان گفت با تبدیل فوریه گرفتن از سیگنال میتوانیم بفهمیم، سیگنال موردنظر در چه فرکانسها یا طیف فرکانسیای مقدار دارد. طبق نظریهی فوریه، هر سیگنالی را میتوان به این طریق به اجزاء فرکانسی سازنده آن تجزیه کرد که به آنها هارمونیک نیز گفته میشود. تعداد این هارمونیکها میتواند یک یا بیشتر باشد. برای روشنتر شدن این موضوع دوباره به همان مثال شکل موج سینوسی برمیگردیم.
یک موج سینوسی از دو جزء تشکیل شده است. یک بخش DC (یا همان آفست سیگنال) و یک بخش AC.
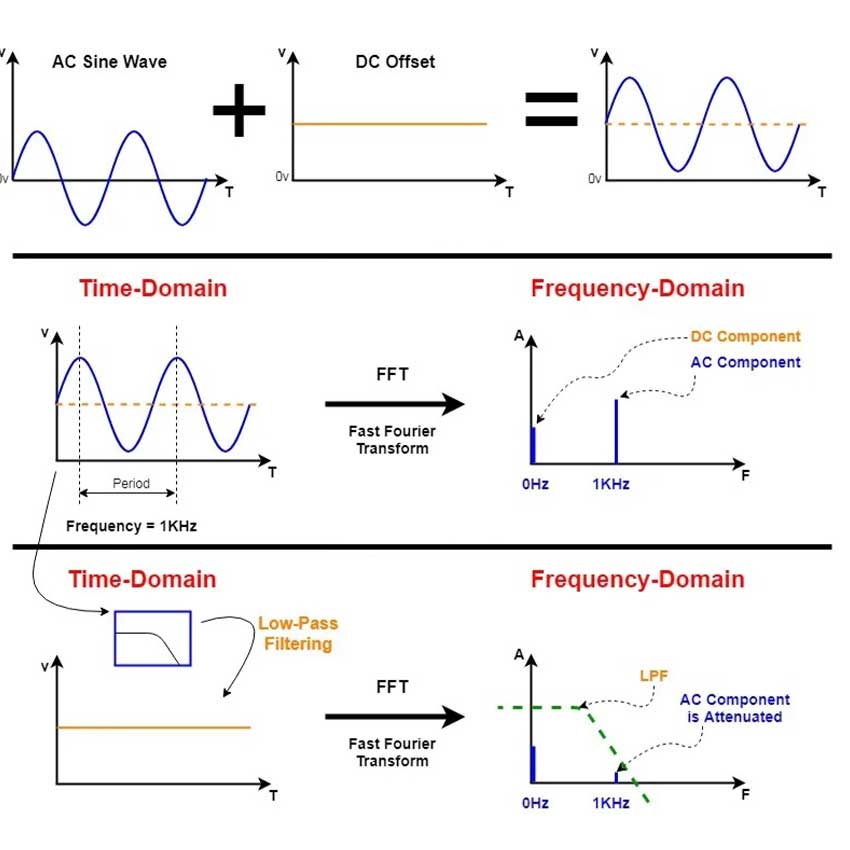
نمایش اجزاء سازنده سیگنال سینوسی در حوزههای مختلف.
در شکل بالا میتوانیم نمایش حوزه فرکانس سیگنال را در قسمت بالا ببینیم. با FFT گرفتن از سیگنال شکل وسط، یعنی نمایش حوزه فرکانس را خواهیم داشت. میبینیم که جزء DC سیگنال در فرکانس 0 هرتز ظاهرشده است و بخش AC نیز در 1kHz در طیف فرکانسی دیده میشود. به نمودار وسط، نمودار حوزه فرکانس گفته میشود. سؤالی که ممکن است پیش بیاید این است که آیا میتوان هر جزء سازنده این سیگنال را، از کل سیگنال جدا کرد و در اختیار داشت؟ جواب این سؤال مثبت است. همانطور که در قسمت پایین شکل نشان داده شده است، مثلاً میتوانیم بخش DC سیگنال را جدا کنیم. برای این منظور سیگنال سینوسی ابتدا از یک فیلتر پایین گذر (LPF) عبور داده میشود و سپس از آن FFT گرفته میشود. در سمت راست شکل میبینیم که جزء AC سیگنال به شکل محسوسی تضعیفشده است (زیرا فیلتر پایین گذر فرکانسهای پایین را عبور داده است و در محدوده فرکانسی 1kHz که فرکانس جزء AC است تضعیف قابلتوجه دارد). پس بدین طریق میتوان بخش DC سیگنال را جدا کرد. در این مثال کاربرد فیلتر کردن و نتیجه آن در حوزه زمان و فرکانس را دیدیم. اکنون میخواهیم کاربرد فیلتر را برای سیگنال PWM بررسی کنیم.
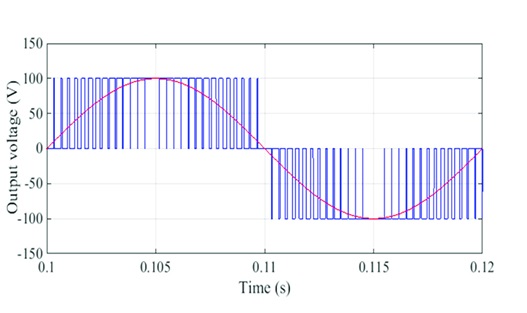
همانطور که قبلاً گفته شد، یک سیگنال PWM درواقع یک موج مربعی است که Duty Cycle آن قابل تنظیم است. حالا اگر بخواهیم در حوزه فرکانس به یک سیگنال PWM نگاه کنیم، طیف فرکانسی وسیعی را مشاهده میکنیم. زیرا چنین شکل موجی از بینهایت هارمونیک مختلف تشکیلشده است. گفتیم بر اساس نظریهی فوریه، هر سیگنالی را میتوان بهصورت مجموعهای از سیگنالهای سینوسی و کسینوسی با فرکانسهای مختلف تجزیه کرد. ازآنجاییکه شکل موج مربعی را بینهایت هارمونیک تشکیل میدهند، با آوردن این سیگنال به حوزه فرکانس چنین چیزی خواهیم دید:
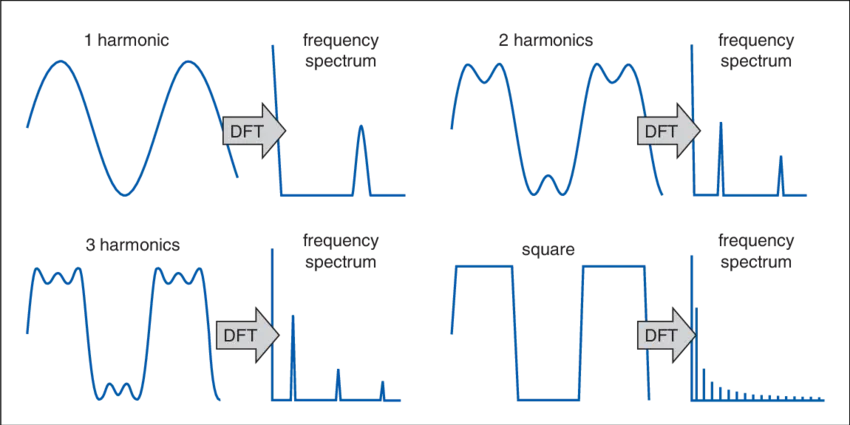
همانطور که در تصویر بالا دیده میشود، به نزدیک شدن شکل موج به موج مربعی، تعداد هارمونیکها بیشتر و بیشتر میشوند و درنهایت در شکل مربعی، تعداد آنها به بینهایت میل میکند. هارمونیکهای سازنده این شکل موجها در تصویر زیر به شکل واضحتری نشان دادهشده است:
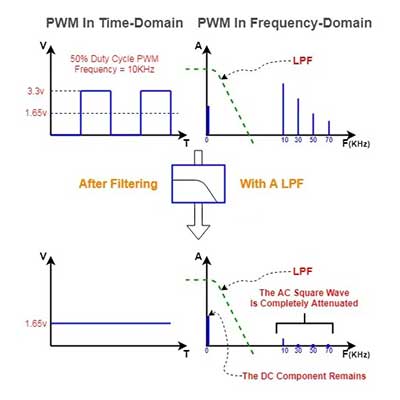
و حالا میرسیم به کاربرد فیلتر کردن برای سیگنال PWM. گفتیم که Duty Cycle یک سیگنال PWM در هر بازه زمانی را میتوان ولتاژ میانگین این شکل موج در نظر گرفت. بهعنوانمثال، یک سیگنال PWM با ولتاژ 3.3 ولت و Duty Cycle 50% را میتوان یک ولتاژ میانگین 1.65 ولت در نظر گرفت. هرچند که میدانیم که یک سیگنال ثابت DC نداریم و سیگنال مابین مقدار 0 تا 3.3 ولت در حال تغییر است.
در وسایلی مثل موتورها و اسپیکرها که بهوسیله موج PWM کنترل میشوند، معمولاً یک فیلتر پایین گذر نیز بهکاررفته است. بدینصورت مثلاً یک سرعت یک موتور، متناسب با تغییرات Duty Cycle موج PWM تغییر میکند. به همین صورت اگر بخواهیم بهوسیله PWM یک DAC بسازیم باید از یک فیلتر پایین گذر استفاده کنیم تا هارمونیکهای AC را حذف کنیم.
در تولید یک شکل موج بهوسیله DAC (که در اینجا PWM نقش آن را بازی میکند)، خروجیای برای ما مطلوب است که توسط میانگین ولتاژ PWM تنظیمشده باشد و حداقل ریپل ممکن را داشته باشد. برای رسیدن به این هدف، باید فرکانس PWM تا جای ممکن بالا باشد و همچنین از فیلتر پایین گذری با فرکانس قطع پایین استفاده کنیم. بدین طریق میتوانیم یک ولتاژ DC پایدار (که همان ولتاژ میانگین PWM است را) از خروجی فیلتر پایین گذر دریافت کنیم.
نکتهی بسیار مهمی که در اینجا باید مراقب آن باشیم، این است که فیلتر استفادهشده بهصورتی است که تمامی المانهای AC را از سیگنال خروجی حذف میکند. درنتیجه سوینگ خروجی به خاطر تأثیر ثابت زمانی بالای فیلتر، بسیار کند خواهد بود. بنابراین DAC ای که ساختهایم توانایی تولید سیگنالهای AC، ازجمله سیگنال سینوسی را نخواهد داشت. این مسئله موجب میشود که مجبور شویم برای تولید شکل موج، توازنی میان فرکانس PWM، فرکانس سیگنالهای خروجی و مشخصات فیلتر پایین گذر، توازن برقرار کنیم.
نحوه ساخت DAC به وسیله PWM
اولین مرحله برای ساخت یک DAC بهوسیله PWM، تعیین دقت (Resolution) موردنیاز برای DAC است. با توجه به اینکه دقت DAC، تعداد سطوح ولتاژی است که خروجی آن میتواند داشته باشد و این تعداد سطوح نیز به PWM بستگی دارد، میتوان گفت که دقت DAC با توجه بهدقت PWM تعریف میشود.
توجه به این نکته حائز اهمیت است که دقت PWM که در دیتاشیت ذکرشده است ثابت نیست. یعنی اینکه دقت PWM در زمان تولید موج تغییر میکند. همانطور که قبلاً اشاره شد، این تغییر دقت به فرکانس شکل موج تولیدی وابسته است. هرچقدر که فرکانس شکل موج خروجی بالاتر باشد، دقت کمتر خواهد شد. درنتیجه با توجه به اینکه چه دقتی برای DAC، برای ما مطلوب است میتوانیم یک حاشیه امن برای تعیین حد بالای فرکانس PWM در نظر بگیریم.
همانطور که پیشتر اشاره شد، در تولید شکل موج، حالت ایدهآل این است که فرکانس PWM به حدی بالا باشد که درنتیجه فیلتر کردن سیگنال آن، کمترین ریپل ممکن در خروجی را داشته باشد. اما بالا بردن فرکانس PWM موجب کاهش دقت خواهد شد، پس چاره چیست؟
انتخاب فرکانس سیگنال PWM
بهعنوان یک قانون ساده برای انتخاب فرکانس سیگنال PWM، میتوانیم همیشه فرکانس PWM را چند درجه بزرگتر از فرکانس سیگنال خروجی موردنظر انتخاب کنیم. در عبارت زیر، هرچقدر که k بزرگتر باشد، نتیجه مطلوبتر خواهد بود؛
![]()
اما همچنان باید توجه داشت که بالا بردن فرکانس PWM موجب کاهش دقت DAC خواهد شد. همانطور که از فرمول ارائهشده برای دقت سیگنال PWM مشخص است، با بالا رفتن فرکانس PWM به ازای هر فرکانس کلاکی، دقت PWM و درنتیجه دقت DAC کاهش خواهد یافت.
طراحی فیلتر پایین گذر RC
مشخصههای دینامیکی DAC ما، توسط فیلتر پایین گذر تعیین میشود. گفتیم که ابت زمانی فیلتر، تأخیر را وارد مدار میکند که سبب میشود سرعت سوینگ DAC کاهش یابد و بدین ترتیب حتی امکان تولید یک شکل موج خاص وجود نداشته باشد. بنابراین در طراحی فیلتر، باید به پارامترهایی توجه کنیم که پاسخ فرکانسی فیلتر را تعیین میکنند. بر همین اساس میتوان سیستم DAC نهایی را به دو نوع DAC استاتیک و DAC دینامیک، تقسیم کرد. در DAC استاتیک از فیلتر پایین گذری با فرکانس قطع بسیار پایین، یعنی در حدود 10 یا 1 هرتز استفاده میشود. در این نوع DAC، سرعت سویینگ خروجی بسیارکم خواهد بود. پس DAC استاتیک برای کاربردهایی مناسب است که نیاز داریم سطوح ولتاژ خاصی را در خروجی تولید کنیم.
در مقابل، DAC دینامیکی دارای فیلتری است که فرکانس سیگنال موردنظر (FBW) را از خود عبور میدهد و فرکانسهای مربوط به هارمونیکهای سیگنال PWM را مسدود میکند. این نوع DAC مناسب تولید شکل موجهای آنالوگ از قبیل موج سینوسی، دندانارهای، مثلثی و … است. برای طراحی چنین فیلتری از فرمول زیر استفاده میشود:
![]() روش صحیح این است که ابتدا مقاومت را براساس قدرت جریان دهی پین GPIO انتخاب کنیم و سپس مقدار خازن را براساس آن، با استفاده از معادله بالا تنظیم کنیم. در پروژه حاضر، ما از یک مقاومت 10 کیلواهم و یک خازن 100 نانوفاراد برای فیلتر استفاده کردهایم. میزان تضعیف فیلتر را میتوان با استفاده از رابطه زیر حساب کرد. درصورتیکه میزان تضعیف فیلتر کافی نباشد، باید فاکتور k که به آن اشاره شد را افزایش دهیم.
روش صحیح این است که ابتدا مقاومت را براساس قدرت جریان دهی پین GPIO انتخاب کنیم و سپس مقدار خازن را براساس آن، با استفاده از معادله بالا تنظیم کنیم. در پروژه حاضر، ما از یک مقاومت 10 کیلواهم و یک خازن 100 نانوفاراد برای فیلتر استفاده کردهایم. میزان تضعیف فیلتر را میتوان با استفاده از رابطه زیر حساب کرد. درصورتیکه میزان تضعیف فیلتر کافی نباشد، باید فاکتور k که به آن اشاره شد را افزایش دهیم.
![]()
درنهایت باید گفت که طراحی فیلتر براساس نیاز و کاربرد میتواند متفاوت باشد و حتی از فیلترهایی با درجه بالاتر استفاده کرد تا سیگنال خروجی به نحو مطلوبتری فیلتر شود. پس طراحی فیلتر باید با توجه به معیارهای پروژه صورت گیرد.
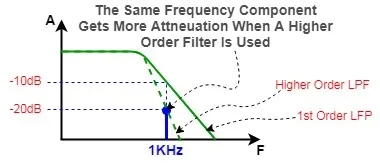
کنترل ولتاژ خروجی DAC
کنترل ولتاژ خروجی DAC به سادگی و با تغییر Duty Cycle سیگنال PWM صورت میگیرد؛
PWM DAC Output Voltage = 3.3 x (CCRx/ARRx)
بافر در خروجی DAC ساخته شده به وسیله PWM
مثل زمانی که از واحد DAC میکروکنترلر استفاده میکنیم. قرار دادن بافر در خروجی DAC حاضر که وسیله PWM ساختهشده است نیز باعث پایدار شدن سیگنال خروجی میشود.
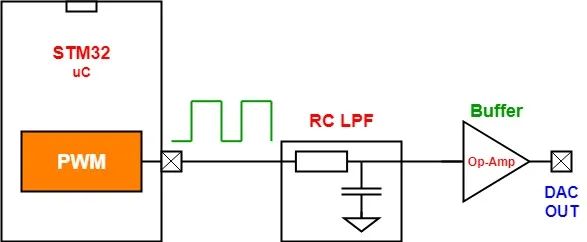
اکنونکه با جزییات تولید شکل موج با سیگنال PWM آشنا شدیم، میخواهیم به سراغ میکروکنترلر برویم و چند شکل موج نمونه تولید کنیم.
نوشتن کد تولید شکل موج
ازآنجاییکه در مرحله قبل، تایمر 1 و کانال PWM آن را فعال کردیم، در این بخش نیازی به تغییر پیکربندی پروژه نیست و میتوانیم به سراغ کد برویم.
تولید شکل موج را با موج ساده مربعی شروع میکنیم. همانطور که مشخص است، با تنظیم Duty Cycle در مقدار 50%، یک موج مربعی خواهیم داشت؛
|
1 |
TIM1->CCR1 = max/2; |
برای تولید موج دادن ارهای، ابتدا در بخش مربوط به تعریف ثابتها، تعداد نمونههای شکل موج را تعریف میکنیم و سپس کد مربوط به تولید شکل موج را در حلقه while(1) مینویسیم؛
|
1 |
#define sample_count 20 //Number of samples |
|
1 2 3 4 5 6 |
/* Sawtooth wave */ for (uint16_t i = 0; i < sample_count; i++) { TIM1->CCR1 = (max * i) / sample_count; HAL_Delay(1); } |
این شکل موج، با توجه به تأخیر استفادهشده و همچنین تعداد نمونهها، فرکانسی برابر با 50Hz خواهد داشت.
برای تولید هر شکل موج این نکته قابلذکر است که برای پیوستگی آنها، لازم است کد مربوط به تولید شکل موجهای دیگر، در حلقه while(1)، کامنت شود.
یادآوری این نکته ضروری است که برای تولید شکل موج دندانارهای (و همچنین شکل موجهای بعدی)، استفاده از فیلتر پایین گذر الزامی است.
به وسیله کد زیر، میتوانیم شکل موج مثلثی (با همان فرکانس 50Hz) تولید کنیم :
|
1 2 3 4 5 6 7 8 9 10 11 |
/* Triangular wave */ for (uint16_t i = 0; i <= (sample_count / 2); i++) { TIM1->CCR1 = ((max * i) / ((sample_count) / 2)); HAL_Delay(1); } for (uint16_t i = (sample_count / 2); i > -1; i--) { TIM1->CCR1 = ((max * i) / ((sample_count) / 2)); HAL_Delay(1); } |
برای تولید شکل موج سینوسی، ابتدا باید قبل از حلقه while(1)، یک Lookup-Table برای موج سینوسی تعریف کنیم؛
|
1 |
const int Sine_Lookup[64] = {0x19,0x1b,0x1e,0x20,0x23,0x25,0x27,0x29, 0x2b,0x2c,0x2e,0x2f,0x30,0x31,0x32,0x32, 0x32,0x32, 0x32,0x31,0x30,0x2f,0x2e,0x2c, 0x2b,0x29,0x27,0x25,0x23,0x20,0x1e,0x1b, 0x19,0x17, 0x14,0x12,0xf, 0xd,0xb,0x9, 0x7,0x6,0x4,0x3,0x2,0x1,0x0,0x0, 0x0,0x0,0x0,0x1,0x2,0x3,0x4,0x6, 0x7,0x9,0xb,0xd,0xf,0x12,0x14,0x17}; |
این شکل موج، از 64 نمونه تشکیلشده است، لذا در صورت استفاده از تأخیر 1 میلیثانیه به ازای هر نمونه، فرکانس موج سینوسی برابر با 15.625Hz خواهد بود؛
Fsin = 1/(TDelay*NSamples) = 1 / 64 * 1ms = 15.625 Hz
اکنون برای تولید شکل موج، در حلقه while(1) کد زیر را مینویسیم:
|
1 2 3 4 5 6 |
/* Sinusoidal wave */ for (uint16_t i = 0; i < 64; i++) { TIM1->CCR1 = Sine_Lookup[i] * max / 0x32; HAL_Delay(1); } |
در آخر نیز برای استفاده از DAC ساختهشده، برای تولید یک شکل موج پلهای، ابتدا یک آرایه برای مشخص کردن مقادیر شکل موج تعریف میکنیم و سپس کد مربوط به تولید موج را در حلقه while(1) مینویسیم؛
|
1 |
uint16_t DAC_OUT[5] = {0, max*1/5, max*2/5, max*3/5, max*4/5}; |
|
1 2 3 4 5 6 |
/* DAC */ for(uint16_t i = 0; i<5; i++) { TIM1->CCR1 = DAC_OUT[i]; HAL_Delay(20); } |
ذکر این نکته حائز اهمیت است که تولید شکل موج بهوسیله PWM از روش دیگری غیر این روش پیادهسازی شده در اینجا نیز امکانپذیر است. در آن روش میتوانیم برای زمانبندی سیگنال از DMA استفاده کنیم. در مورد DMA، در قسمتهای آینده صحبت خواهیم کرد.
حالت پیشرفته PWM
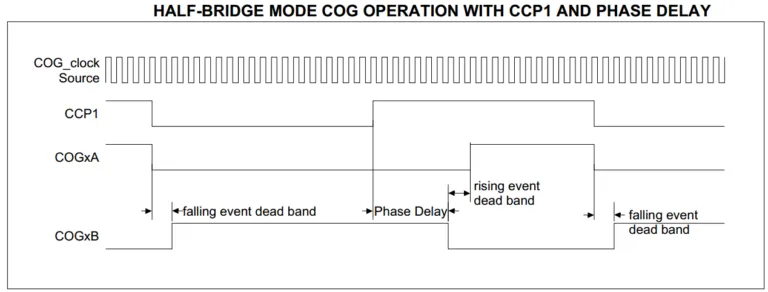
حالت پیشرفته تولید سیگنال PWM، شامل مدارها و کنترل سختافزاری بیشتر برای تنظیم پارامترها و جزییات پیشرفتهتر، برای تولید سیگنال است. این ویژگیها شامل موارد زیر میشوند:
- قابلیت تولید سیگنال PWM متمم، که همان سیگنال تولیدشده در کانال اصلی است، با این تفاوت که منطق آن معکوس شده است.
- امکان اضافه کردن Dead-time band در سیگنال PWM، که در کاربردهایی مثل درایو موتور و باهدف جلوگیری از جریان shoot-through کاربرد دارد.
- قابلیت انجام auto-shutdown برای سیگنال PWM. این قابلیت که بانام auto brake نیز شناخته میشود در کاربردهای نیازمند به ایمنی بالا، اهمیت دارد.
- امکان انجام phase-adjust در سیگنال PWM.
- و…
در شکل زیر یک مثال از خروجی کانالهای PWM در حالت تولید شکل موج متمم، با اعمال dead-time و تنظیم phase-delay نشان داده شده است. این سیگنال، یک سیگنال کنترلی نمونه برای حالت half-bridge است.
در این قسمت از سری آموزش STM32 با توابع HAL، با PWM آشنا شدیم و همچنین نحوه تولید شکل موج توسط آن را یاد گرفتیم. در قسمت بعدی در مورد تایمرهای نگهبان مستقل و پنجرهای (IWDG و WWDG) صحبت خواهیم کرد. با ما همراه باشید.

حالت Input capture و حالت Output compare در...

تایمرهای نگهبان IWDG و WWDG در STM32 |...


















سیسوگ با افتخار فضایی برای اشتراک گذاری دانش شماست. برای ما مقاله بنویسید.