اهمیت تئوری و ریاضیات در برنامه‌نویسی قسمت دوم: کری یا سرریز، کدام؟

در قسمت اول این مجموعه از مقالات، سیستم مکمل 2 را که همه‌ی ما از دوران دانشگاه از درس مدار منطقی با آن آشنا هستیم، به خوبی واکاوی کردیم و از خاصیتی نهفته در دل این سیستم پرده برداشتیم و مفصلا توضیح دادیم که این خاصیت نهفته چه کاربردی می‌تواند داشته باشد. همچنین در نهایت یک مثال را در میکروکنترلر AVR که رجیسترهای این نوع از میکروکنترلرها 8 بیتی هستند، بررسی کردیم و ادعای خود مبنی بر همان خاصیت نهفته در دل سیستم متمم 2 رابه اثبات رساندیم.

در قسمت قبل یکی از دوستان با ادمین کانال تلگرام سیسوگ مرتبط شدند و اشاره کردند که اسم این خاصیت که سیستم متمم 2 را منحصر به فرد کرده است، wraparound نام دارد. بله این دوست عزیز درست فرمودند و اسم این خاصیت مهم wraparound نام دارد. اما ما چون می‌خواستیم همین موضوع را بیشتر توضیح داده و البته موضوعی دیگر را نیز بیان کنیم، صبر کردیم تا در این قسمت موضوعی دیگر را بیان کنیم و در قسمت بعد، از تر کیب این دو موضوع مثالی کاربردی‌تر و البته بسیار جذاب، برای شما ارائه بدهیم.

شاید برای شما مفید باشد: آموزش FPGA

این مقاله هم مانند مقاله قسمت قبل به نکته‌ای نهفته در درون اعداد اشاره می‌کند و یک اشتباهی که نه تنها دانشجویان، بلکه بسیاری از افراد با تجربه در حوزه الکترونیک نیز تکرار می‌کنند را یادآور می‌شود.

آیا بین کری (carry) و سرریز (overflow) تفاوتی وجود دارد؟

شاید بنا به یک دلیل بعضی افراد فکر کنند که بین این دو پارامتر هیچ تفاوتی وجود ندارد، اما این دلیل به کجا برمی‌گردد؟ اگر به خاطر داشته باشید اولین بار در درس مدار منطقی سیستم اعداد بدون علامت به ما آموخته شده است، در این سیستم هیچ تفاوتی بین کَری و سرریز وجود نداشت و می‌گفتیم هر موقع کری داشته باشیم سرریز رخ داده است یا اینکه کری و سریز یکی هستند. بعد از آن، سیستم علامت و مقدار و بقیه‌ی سیستم‌های علامت‌دار به ما آموخته شد، مسئله همینجا پیش می‌آید، حال در سیستم اعداد علامت‌دار آیا کری و سرریز یکی هستند؟

خیر، در سیستم اعداد علامت‌دار کری و سرریز یکی نیستند و شاید دلیل این اشتباه که بعضی از افراد فکر می‌کنند در سیستم اعداد علامت‌دار این دو پارامتر یکی هستند این باشد که هنگامی که درس مدار منطقی را می‌گذراندند، وقتی از سیستم اعداد بدون علامت گذر کردند و به سیستم اعداد علامت‌دار رسیدند، به آن‌ها تعریف جدید گفته نشد و همان تعریف قبلی را به سیستم اعداد علامت‌دار نیز تعمیم دادند که خود اشتباه است و یا اگر گفته شد خیلی سطحی و سرسری بیان شد، چون اگر این موضوع به خوبی بیان می‌شد و گفته می‌شد که چه کاربردی دارد، تقریبا محال ممکن است که افراد به اشتباه فکر کنند در سیستم اعداد علامت‌دار هم کری وسرریز یکی هستند.

رابطه بین کری و سرریز در سیستم اعداد متمم 2

برای اینکه بتوانیم این موضوع را در سیستم اعداد علامت‌دار شرح بدهیم، سیستم متمم 2 که تا به امروز بهترین و بهینه‌ترین سیستم شناخته‌شده در نمایش اعداد در دیجیتال می‌باشد را انتخاب کردیم. در سیستم اعداد متمم 2، در رابطه با کری و سرریز، چهار حالت ممکن است به وجود بیاید که به تشریح هر کدام از این حالت‌ها به صورت دقیق خواهیم پرداخت. اما قبل از آن اجازه بدهید به تنها حالت ممکن که در سیستم اعداد بدون علامت وجود دارد بپردازیم.

کری و سرریز در اعداد بدون علامت

فرض کنید می‌خواهیم دو عدد بدون علامت 3 بیتی را با هم جمع کنیم، اعداد 4+ و 5+ را در نظر می‌گیریم. طبق تصویر زیر آن‌ها را با هم جمع می‌کنیم.

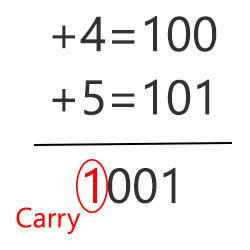
همانطور که از تصویر بالا مشخص است چون جمع نهایی در محدوده نبوده است، سرریز رخ داده است و بیت کری هم داریم.

حال با این توضیحات سراغ مثال‌هایی در سیستم متمم 2 می‌رویم تا نشان دهیم که وجود یا عدم وجود کری به هیچ وجه نمی‌تواند نشان‌دهنده‌ی وجود سرریز باشد.

در مثال‌های زیر ما عرض بیت را 3 بیت تعیین کردیم، یعنی محدوده اعدای که با این تعداد بیت می‌توانیم نمایش بدهیم از 4- تا 3+ می‌باشد.

نه کری داریم و نه سرریز رخ داده است

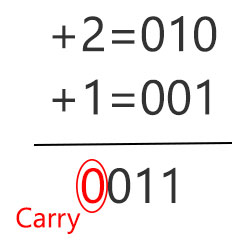
خب در این حالت اتفاق خاصی نیفتاده است و دو عدد طبق روال معمول باهم جمع شده‌اند.

کری داریم ولی سرریز رخ نداده است

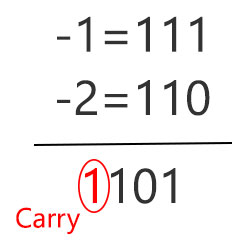
در تصویر بالا کری وجود دارد، اما همانطور که گفتیم صرفا وجود کری نمی‌تواند مشخص کند که سرریزی رخ داده است یا خیر.

کری نداریم اما سرریز رخ داده است

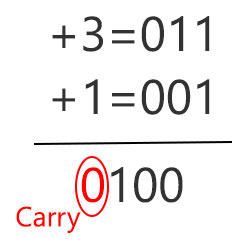
در تصویر بالا کری وجود ندارد، اما می‌دانیم که جمع این دو عدد در محدوده‌ی قابل نمایش توسط 3 بیت نمی‌گنجد و سرریز رخ داده است.

هم کری داریم و هم سرریز رخ داده است

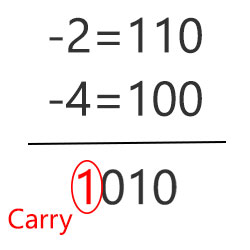
در تصویر بالا کری وجود دارد، سرریز نیز رخ داده است، این حالت مشابه با اعداد بدون علامت می‌باشد که وجود کری مشخص‌کننده‌ی رخ دادن سر ریز است. اما در نظر بگیرید که این حالت، فقط یک حالت از چهار حالت ممکن می‌باشد و صرفا وجود کری نمی‌تواند مشخص کند که سرریز رخ داده است یا خیر.

پس تا اینجا متوجه شدید که جز در حالتی خاص کری و سرریز هیچ ارتباطی با همدیگر ندارند و دو چیز جدا از هم هستند. اما بهتر است که دو تعریف کلی و مجزا برای این دو پارامتر ارائه بدهیم تا در فهمیدن و تشخیص این موارد دچار اشتباه و سردرگم نشویم.

اینکه چگونه کری و سرریز را تشخیص بدهیم و چه عملیاتی روی آن‌ها انجام بدهیم تا بتوانیم سرریز را کنترل کنیم، چه مواقعی نیاز به کنترل سرریز نمی‌باشد و اگر نیاز است که کنترل کنیم با چه روش‌هایی و چگونه می‌توانیم سر ریز را کنترل کنیم، روش‌های wrapping و saturation در کنترل سرریز چیست و کلی سوال دیگر از جمله سوالاتی هستند که هم در قسمت سوم پاسخ داده خواهند شد و هم اینکه به صورتی عملی همراه با مثال روی میکروکنترلر یا fpga تست خواهند شد.