آنالیز جریان مش تکنیکی است که برای یافتن جریان‌های در حال گردش در اطراف یک حلقه یا مش در هر مسیر بسته از مدار استفاده می‌شود. درحالی‌که قوانین کیرشهف روش اساسی را برای تجزیه‌وتحلیل هر مدار پیچیده الکتریکی به ما ارائه می‌دهد، روش‌های مختلفی برای بهبود این روش با استفاده از آنالیز جریان مش یا آنالیز ولتاژ گره‌ای وجود دارد که منجر به کاهش ریاضی درگیر و هنگامی‌که شبکه‌های بزرگ درگیر هستند این کاهش ریاضیات می‌تواند یک مزیت بزرگ باشد.
به عنوان مثال، مثالِ مدار الکتریکی را از بخش قبلی در نظر بگیرید.
مدار آنالیز جریان مش
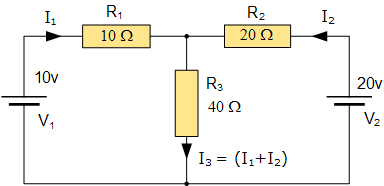
یک روش ساده برای کاهش میزان ریاضیات، آنالیز مدار با استفاده از معادلات قانون جریان کیرشهف برای تعیین جریان I1 و I2 در دو مقاومت است. پس‌نیازی به محاسبه I3 نیست چون فقط جمع I1 و I2 است. بنابراین قانون ولتاژ دوم Kirchhoff به‌سادگی تبدیل می‌شود:
- Equation No 1 : 10 = 50I1 + 40I2
- Equation No 2 : 20 = 40I1 + 60I2
بنابراین، یک خط محاسبات ریاضی ذخیره شده است.
آنالیز جریان مش
یک روش آسان‌تر برای حل مدار فوق با استفاده از آنالیز جریان مش یا آنالیز حلقه است که گاهی اوقات به آن روش جریان‌های در حال گردش Maxwell نیز می‌گویند. به‌جای برچسب زدن جریان‌های شاخه‌ای، باید هر “حلقه بسته” را با جریان درج‌شده برچسب‌گذاری کنیم. به‌عنوان یک قاعده کلی، فقط حلقه‌ها را در جهت عقربه‌های ساعت با جریان‌های در حال چرخش برچسب بزنید زیرا هدف این است که حداقل یک‌بار تمام عناصر مدار را بپوشانید. هرگونه جریان انشعاب موردنیاز را می‌توان از حلقه یا جریان مش مناسب مانند قبل با استفاده از روش کیرشهف یافت.
For example: i1 = I1 , i2 = -I2 and I3 = I1 – I2
ما اکنون معادله قانون ولتاژ کیرشهف را به همان روش قبلی برای حل آنها می‌نویسیم اما مزیت این روش این است که اطمینان حاصل می‌کند که اطلاعات به‌دست‌آمده از معادلات مدار، حداقل موردنیاز برای حل مدار است زیرا اطلاعات عمومی‌تر است و می‌تواند به‌راحتی در قالب ماتریس قرار بگیرد.
شاید برای شما مفید باشد : آموزش الکترونیک از 0 تا 100 کاملا رایگان
به عنوان مثال، مدار مربوط به بخش قبلی را در نظر بگیرید.
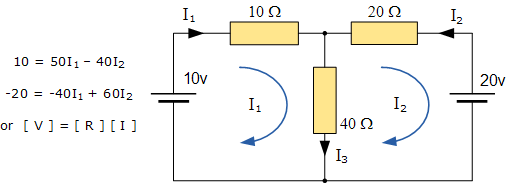
این معادلات را می‌توان با استفاده از یک ماتریس امپدانس تک شبکه Z به‌سرعت حل کرد. هر عنصر روی قطر اصلی “مثبت” خواهد بود و کل امپدانس هر مش است. در صورت وجود، هر عنصر خاموش قطر اصلی “صفر” یا “منفی” خواهد بود و نشان‌دهنده عنصر مدار است که تمام مش‌های مناسب را متصل می‌کند. ابتدا باید درک کنیم که هنگام کار با ماتریس، برای تقسیم دو ماتریس، همان ضرب یک ماتریس در معکوس ماتریس دیگر است همان‌طور که نشان داده‌شده است.
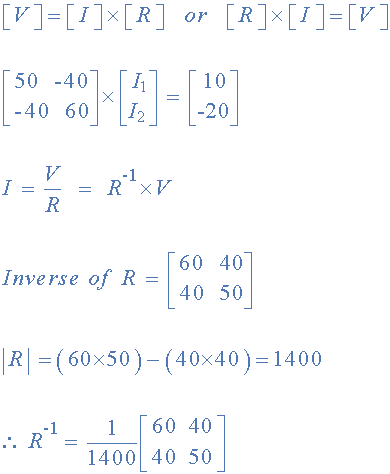
با پیدا کردن معکوس R، چون V/R همان V x R-1 است، اکنون می‌توانیم از آن برای یافتن دو جریان در گردش استفاده کنیم.
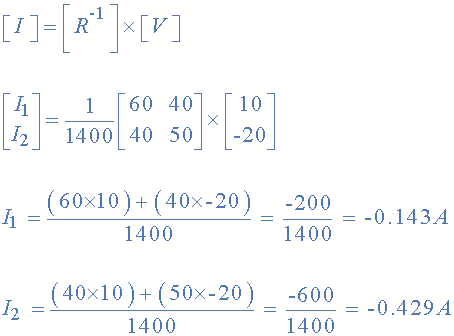
بنابراین:
- [ V ] ولتاژ کل باتری را برای حلقه 1 و سپس حلقه 2 می‌دهد
- [ I ] نام جریان‌های حلقه را بیان می‌کند که می‌خواهیم آنها را پیدا کنیم
- [ R ] ماتریس مقاومت است
- [ R-1 ] وارون ماتریس [R] است
و این I1 را 0.143- آمپر و I2 را 0.429- آمپر می‌دهد.
As : I3 = I1 – I2
جریان ترکیبی I3 بدین ترتیب ارائه می‌شود: (0.429-) – 0.143- = 0.286 آمپر
این همان مقدار جریان 0.286 آمپر است که قبلاً در آموزش قانون مدار کیرشهف پیدا کردیم.
خلاصه
این روش “نگاه کردن” برای تجزیه‌وتحلیل مدار، احتمالاً بهترین روش برای تجزیه‌وتحلیل مدار با روش اصلی، برای حل معادلات تجزیه‌وتحلیل جریان مش به شرح زیر است:
- تمام حلقه‌های داخلی را با جریان‌های چرخشی برچسب‌گذاری کنید. (I1, I2, …IL و غیره)
- ماتریس ستون [L x 1] [V] را بنویسید که مجموع تمام منابع ولتاژ را در هر حلقه ارائه می‌دهد.
- ماتریس [L x L]، [R] را برای تمام مقاومتهای مدار به صورت زیر بنویسید:
- R11 = مقاومت کل در حلقه اول
- Rnn = مقاومت کل در حلقه N
- RJK = مقاومتي كه مستقيماً حلقه J را به حلقه K مي‌پيوندد.
- معادله ماتریس یا بردار [V] = [R] x [I] را در جایی بنویسید که [I] لیستی از جریان‌های یافت شده است.
همچنین با استفاده از تحلیل جریان مش، ما همچنین می توانیم برای محاسبه ولتاژهای حلقه ها از تجزیه و تحلیل گره استفاده کنیم، و این مقدار یاضیات مورد نیاز را فقط با استفاده از قوانین کیرشهف کاهش می دهد. در آموزش بعدی مربوط به تئوری مدار DC، برای انجام این کار به تحلیل ولتاژ گره ای خواهیم پرداخت.
