شرح مسئله فازی Fuzzy logic به همراه مثال حل مسئله فازی
تعریف سیستم فازی
منطق فازی؛ استدلال مبهم fuzzy logic شکلی از منطقهای چند ارزشی بوده که در آن ارزش منطقی متغیرها میتواند هر عدد حقیقی بین ۰ و ۱ و خود آنها باشد. بهطوری که میزان درستی میتواند هر مقداری بین کاملاً درست و کاملاً غلط باشد. اصطلاح منطق فازی اولینبار در پی تنظیم نظریه مجموعههای فازی بهوسیله لطفیزاده (۱۹۶۵ م) در دنیای محاسبات جدید ظاهر شد.
واژه فازی به معنی: غیردقیق، ناواضح و مبهم (شناور) است. نظریه فازی در یک نگاه اول به نظریه احتمال و فضای حالت آن نزدیک است؛ ولی در عین شباهت دو دنیای کاملا متفات هستند با من همراه باشید تا با یک مثال به شرح کامل سیستم های فازی بپردازیم. امیدوارم در پایان این مقاله به درک کاملی از منطق فازی و سیستم فازی برسید.
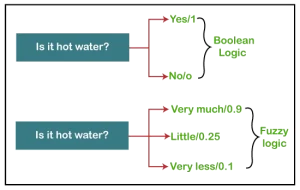
منطق فازی
بررسی تفاوت میان این دو نظریه – احتمالات و فازی
در عین پیچیدگی بیان تفاوت های میان دو نظریه احتمالات و فازی، بسیار ساده می باشد. منطق فازی با حقایق نادقیق سروکار دارد و به حد و اندازه یک واقعیت اشاره دارد؛ حالآنکه نظریه احتمالات بر شالوده مجموعه حالات تصادفیِ یک پدیده استوار است و درباره شانس وقوع یک حالت خاص صحبت میکند؛ حالتی که در صورت وقوع آن احتمال آن 100% می شود.
ذکر یک مثال میتواند موضوع را روشن کند. فرض کنید در حال رانندگی در یک خیابان هستید. اتفاقاً متوجه میشوید که کودکی در اتومبیل دیگری که بهموازات شما در یک خودرو در حال حرکت است، نشسته و سر و یکدست خود را از پنجره ماشین بیرون آورده و در حال بازیگوشی است. این وضعیت واقعی است و نمیتوان گفت احتمال اینکه بدن این کودک بیرون اتومبیل باشد، چقدر است.
چون بدن او واقعاً بیرون ماشین است، ولی بدن وی کاملاً خارج از خودرو نیست، بلکه فقط بخشی از بدن او در خارج اتومبیل قرار گرفته است. تئوری احتمالات در اینجا کاربردی ندارد. چون ما نمیتوانیم از احتمال خارج بودن بدن کودک از ماشین صحبت کنیم؛ زیرا در کل فرض غلطی است. اما میتوانیم از احتمال وقوع حادثه صحبت کنیم. مثلاً هرچه بدن کودک بیشتر بیرون باشد، احتمال اینکه در اثر برخورد با بدنه یک اتومبیل در حال حرکت دچار آسیب شود، بیشتر میشود. این حادثه هنوز اتفاق نیفتاده است، ولی میتوانیم از احتمال وقوع آن صحبت کنیم. اما بیرون بودن تن کودک از ماشین همین حالا به واقعیت تبدیل شده است و فقط میتوانیم از میزان و درجات آن صحبت کنیم.
عدم امکان بیان عددی برای کیفیت رویدادها
تفاوت ظریف و درعینحال پررنگی میان نظریه احتمالات و نظریه فازی وجود دارد که اگر دقت نکنیم، دچار اشتباه میشویم؛ زیرا این دو نظریه معمولاً در کنار یکدیگر و در مورد اشیای مختلف همزمان مصداقهایی پیدا میکنند. هنگامی که به یک پدیده مینگریم، نوع نگاه ما به آن پدیده میتواند تعیین کند که باید درباره احتمالات صحبت کنیم یا منطق فازی.
در مثال فوق موضوع دغدغه ما کودکی است که در حال بازیگوشی است. اما یکوقت نگران این هستیم که تا چه اندازه خطر او را تهدید میکند. خطری که هنوز به وقوع نپیوسته است. یکوقت هم ممکن است نگران باشیم که بدن او چقدر بیرون پنجره است. واقعیتی که هماکنون به وقوع پیوسته است.
نگاه راهحل فازی در یک مسئله:
فرض مسئله ساده فرماندادن به یک فن برای واکنش به گرمای محیط.
- صورتی از مسئله است که بهسادگی با رسیدن به دمای گرم روش و سرد خاموش بشود. (اعداد مطلق با فقط با یک برابری قیاس شوند. مثلاً دما به آستانه عددی رسید فن روش در غیر این صورت خاموش بشود.)مشکل اینجاست که در حدود و نزدیک آستانه فن بهدفعات و سرعت زیادی خاموش روش خاموش خواهد شد و رفتار خوبی نخواهد داشت. نمودار .A
- استفاده از اشمیت تر پیگیرها کمک به حل مشکل میکند. ولی حتماً خروجی خاموش و روشنشدن فن باعث میشود دما هم در یک بازهای که اشمیت درگیر تریشولد میشود نوسان داشته باشد (در حدود آستانه روشن و با یک بازهای جداگانه خاموش شود.) نمودارB

نگاه راهحل فازی در یک مسئله
U: نمودار دمای واقعی و آنالوگ
A: پاسخ تریشولد
B: پاسخ اشمیت تریگی (خطقرمز دمای تریشولد، آستانه واکنش – خطوط سبز آستانهبالا و پایین هستند)
** تعداد فرمانهای برای خاموش و روشنشدن فن در نمودار B حدود نصف شده است.
3. راهحل استفاده سیستمهای با استفاده از ضرایب پسخور مانند PID

راهحل استفاده سیستمهای با استفاده از ضرایب پسخور مانند PID
قیاس این دو روش و حتی ترکیب این دو روش بسیار بحثبرانگیز هست و نتایج خیلی خوبی را در دسترس خواهد داشت.
می توانید برای اطلاعات بیشتر به وبسایت Reaserch gate مراجعه نمایید.
و یا برای ترکیب این دو میشود دیاگرام زیر را متصور بود. حالتهای مختلفی دیگری هم پیادهسازی و یا شبیهسازیشده است که هدف بهینهسازی ضرایب بیشتر بوده است.
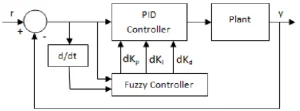
دیاگرام ترکیب سیستم فازی و احتمال
نگاه فازی
برای تعریف فازی مسئله اول ابتدا نیاز داریم آستانه یا آستانهها را در همان حالت در این Solution را بهوسیله توابعی تعریف کنیم.
من سه حالت سرد، گرم، معتدل را تعریف میکنم. (حالتهای بیشتری هم قابلتعریف هستند که در انتها خروجی تمام توابع با هم اجتماع، جمع خواهند شد.) الان بهجای اعداد توابعی را تعریف میکنم.
توابع خروجی بین ۰ و یک به من میدهند. معمولاً این شش تابع بهعنوان برازش یا رول (Rule) یا عضویت انتخاب میشوند.
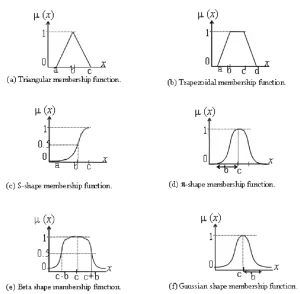
نگاه فازی
ولی شرط کلی توابع بودن و خروجی بین صفر و یک باید باشد که منظور این است که عدد ورودی برای این مسئله خاص چقدر عضویت دارد و یا بهمنظور ما در این حالت نزدیم و درست است.

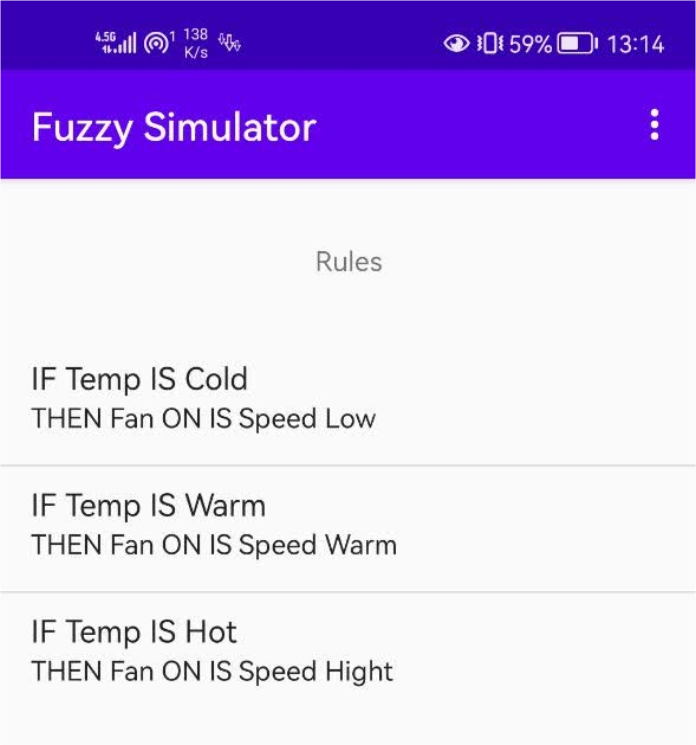
نرمافزار Fuzzy simulator APK3
میگویم دمای معتدل دمای بین ۱۸ تا ۲۴ درجه هست. (دمای قطعی معتدل ۲۱ میشود) به نظر تابعی گوسین بهخوبی نظرمان را پوشش میدهد.
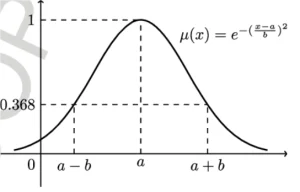
نگاه فازی 3
برای راحتی ادامه بحث و داشتن نتیجه ملموس من از تابع مثلثی استفاده میکنم (Triangle) شبیهساز اندرویدی در دسترس فقط این حالت را پشتیبانی میکرد. ولی با متلب شبیهساز با دستور FIS اجرا و تقریباً حالات زیادی را پشتیبانی میکند.
در ادامه حالتهای سرد و معتدل را بهصورت زیر تعریف میکنیم. در واقع در زبان غیردقیقی سعی در تعریف حالات را میکنیم برای ورودی (linguistics) . پس در یک بخش دما ورودی و در یک پاسخ خروجی (یک یا چند خروجی، مثلاً فن و زاویه پنجره و حتی مثلاً ارسال خطای دما به موبایل و …)
شکل در نرمافزار Fuzzy simulator APK
- نرمافزار Fuzzy simulator APK2
- نرمافزار Fuzzy simulator APK3
- نرمافزار Fuzzy simulator APK1
برای خروجی فن نیز داریم.
- در واقع انتظار داریم عددی بین ۰ تا ۵۰ برای دما وارد کنیم.
- حال عدد را در سه تابع (بهصورت پارالل مثلاً) میگذاریم و عدد عضویت همه توابع را اجتماع میگیریم. تا اینجا میتوانیم عددی را به دست بیاوریم که به ما میگوید چه عددی در مبنای تعاریف ما عدد درستی برای عضویت توابع است و اینجا یک عددی داریم در مبنای فازی و برای استفاده از آن باید تعریف کنیم که این عدد چه معنا یا معناهایی میدهد. مثلاً برای این عدد واکنش یک فن را در نظرمیگیریم یا مثلاً ارسال پیام اخطار با کاربر یا متنیهای مرتبط
- در اینجا برای نمونه یک فن را تعریف میکنیم – با سه حالت، که خروجی محاسبه قبلی را دوباره با این تعاریف برای داشتن خروجی سرعت فن وارد میکنیم. راهحل استفاده سیستمهای با استفاده از ضرایب پسخور مانند PID
- حال برای داشتن خروجی باید رولها یا برازشها را تعریف کنیم.
- خروجی فن 2
- خروجی فن
5. به طور مثال در خط اول میگوییم. اگر دما سرد هست، فن در مجموعه سریع هست. حتی میشود حالت ارسال پیام هم فرضی برای خروجی دید و برای ان قاعده ایی ساخت.
6. حال برای خروجی شبیهسازی میکنیم و نتیجه را میبینیم. برای عدد ۲۷ ورودی دما عدد ۳۵٫۸۹ در مبنای عدد 0 تا 50 هست. (عدد 27 مشترک در مجموعه گرم و معتدل هست و خروجی ان برای فن میشود ۳۵٫۸۹)
- شبیهسازی
- شبیهسازی
نگاه روشهای حال مسئله در NP
مروی به این اصطلاحات را در این حوزه را به شما پیشنهاد میدهم.
محدودسازی (restriction)
با محدودسازی ساختمان دادههای ورودی (مثال: گراف مسطح)، معمولاً الگوریتمهای سریعتر قابلاستفاده خواهند بود.
تصادف سازی (Randomization)
از تصادفیسازی برای بهدستآوردن زمان اجرای میانگین سریعتر استفاده میشود. همچنین به الگوریتم اجازه میدهند که برخی از احتمالات کم و بیاهمیت را نادیده بگیرد.
تقریب سازی (Approximation)
بهجای جستجو برای راه بهینه، به دنبال نزدیکترین بهواقع باشیم.
مکاشفهای (Heuristic)
پاسخی به ما میدهد که به طور منطقی در بسیاری از حالات خوب هستند، ولی هیچ تضمینی بر این نیست که همواره پاسخ صحیح و بهینه را بدهند.
پارامترسازی (Parameterization)
اگر برخی از پارامترها ثابت باشند، معمولاً راهحلهای سریعی هستنa
























سیسوگ با افتخار فضایی برای اشتراک گذاری دانش شماست. برای ما مقاله بنویسید.