مقدمه
یکی از مهمترین مزایای طراحیهای مبتنی بر تراشههای قابل پیکرهبندی توانایی آنها در پیادهسازی الگوریتمهای ریاضی به بهترین شکل ممکن است. برای مثال اگر برای دستیابی به پاسخ نهایی محدودیت زمانبندی وجود دارد، میتوان از پایپلاین کردن در بین گامهای اجرای محاسبات استفاده کرد. اما اگر دقت نهایی اهیمت بیشتری دارد، میتوان از تعداد بیتهای بیشتری برای دستیابی به دقت مطلوب استفاده کرد. البته تقریبا تمامی تراشههای قابل پیکرهبندی مجهز به بلوکهای ضرب کننده DSP هستند که کمک فراوانی به پیادهسازی بهینه الگوریتمهای ریاضی میکند. در این آموزش قصد داریم مروری بر مبانی محاسبات ریاضی در FPGA داشته باشیم. اجازه بدهید با هم نگاهی بیاندازیم به قوانین و تکنیکهایی که شما میتوانید برای توسعه یک تابع ریاضی روی تراشههای قابل پیکرهبندی بکار بگیرد.
شاید برای شما مفید باشد: آموزش FPGA
نمایش اعداد
در حالت کلی دو الگوی کلی برای نمایش اعداد درون یک طراحی دیجیتال وجود دارد.
- سیستم نمایش اعداد ممیز ثابت و
- سیستم نمایش اعداد ممیز شناور.
سیستم نمایش ممیز ثابت، موقعیت نقطه اعشار را ثابت نگه میدارد، به این ترتیب میتوان عملیات ریاضی را کاملا سرراست انجام داد. مهمترین نقطه ضعف سیستم ممیز ثابت این است که برای نشان دادن اعداد بزرگتر با هدف رسیدن به نتیجه دقیقتر باید از تعداد بیت بیشتری برای نمایش بخش اعشاری استفاده کرد. هر عدد ممیز ثابت از دو بخش صحیح و اعشاری تشکیل شده است.
در سیستم نمایش ممیز شناور، نقطه اعشار با توجه به اندازه عدد، میتواند به مکانهای مختلف در داخل عدد منتقل یا در اصطلاح شناور شود. اعداد ممیز شناور نیز به دو بخش مانتیس و توان تقسیم میشوند. این سیستم نمایش بسیار شبیه به شیوه نمایش علائم علمی است، که در آن عدد A را به صورت ضریبی برای عدد پایه ۱۰ به توان B نشان داده میشود. در اینجا A معرف مانتیس و B نماینده توان یا نما است. با این تفاوت که، پایه مورد استفاده برای نمایش در یک عدد ممیز شناور برابر با ۲ است، یعنی A ضربدر ۲ به توان B. اعداد ممیز شناور توسط IEEE/ANSI standard 754-1985 استاندارد شدهاند. در نمایش استاندارد یک عدد ممیز ثابت ۸ بیت به نمایش توان و ۲۴ بیت برای نمایش مانتیس اختصاص داده شده است.

شکل (۱) نحوه نمایش اعداد ممیز شناور برگرفته از IEEE برای انجام محاسبات ریاضی
به دلیل پیچیدگی سیستم اعداد ممیز شناور، ما به عنوان طراح هر جا ممکن باشد از نمایشهای ممیز ثابت استفاده میکنیم. عدد ۱۶ بیتی ممیز ثابت زیر قادر به نمایش اعداد بدون علامت در بازه 0.0 تا 255.9906375 است. در صورت علامت دار بودن قادر به نمایش اعداد بین 128.9906375- تا 127.9906375 بر اساس روش نمایش مکمل دو است. درون طرح شما به عنوان طراح با توجه به الگوریتمی که در حال پیادهسازی آن هستید، انتخاب میکنید که از اعداد علامت دار یا بدون علامت استفاده کنید.
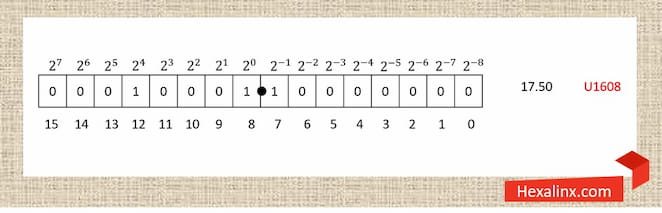
شکل (۲) نمایش ۱۶ بیتی عدد 17.5 با فرمت U1608
دامنه تغییرات اعداد علامت دار و بدون علامت با هم متفاوت است. برای اعداد بدون علامت دامنه تغییرات محدود به بازه صفر تا 2N-1 است. اما در مقابل، دامنه تفییرات یک عدد علامت دار با توجه به روش نمایش آن متغیر است. اعداد علامت دار با توجه به یکی از روشهای علامت اندازه، مکمل یک و مکمل دو نمایش داده میشوند.
در روش نمایش علامت و اندازه از بیت چپ برای نشان دادن علامت عدد (0 = مثبت ، 1 = منفی) استفاده میشود. بیتهای باقیمانده اندازه را نشان میدهند. بنابراین، در این شیوه نمایش، اعداد مثبت و منفی دارای اندازه یکسان هستند اما بیت علامتشان متفاوت است. در نتیجه، این روش نمایش دارای دو مقدار صفر است یعنی درای یک صفر مثبت و منفی است.
نمایش اعداد مثبت در روش مکمل یک مشابه روش علامت اندازه است، اما برای اعداد منفی از وارونگی (مکمل یک) عدد مثبت استفاده میشود.
اگر با FPGA آشنایی ندارید اول مقاله FPGA چیست؟ را مطالعه نمایید.
محاسبات ممیز ثابت
چندین روش برای نشان داده فرمتهای ممیز ثابت استفاده میشود، فرمت مرسوم نمایش بیتهای صحیح و اعشاری در یک عدد ممیز ثابت به صورت نمایش x,y است که در آن x تعداد بیتهای صحیح و y تعداد بیتهای اعشاری را نشان میدهد. به عنوان مثال عددی با فرمت 8,8 دارای ۸ بیت صحیح و ۸ بیت اعشار است، در حالی که فرمت 16,0 نمایانگر اختصاص ۱۶ بیت صحیح و صفر بیت اعشار است. در بسیاری از موارد، طراح تعداد بیتهای بخش صحیح و بخش اعشاری را در زمان طراحی را تعیین میکند، فرایند ممیز ثابت کردن عموما بر اساس یک الگوریتم ممیز شناور صورت میپذیرد و در آن ما به دنبال تبدیل یک الگوریتم ممیز شناور به الگوریتم ممیز ثابت هستیم.
به لطف انعطافپذیری FPGA ها، ما میتوانیم عدد ممیز ثابت را با هر طول بیتی نشان دهیم. تعداد بیتهای بخش صحیح بستگی به اندازه بزرگترین عدد صحیح مورد نیاز در محاسبات دارد. در حالی که تعداد بیتهای بخش اعشاری به صحت و دقت مورد نیاز برای محاسبات وابسته است.
قوانین محاسبات ممیز ثابت
جمع، تفریق یا تقسیم
برای جمع، تفریق یا تقسیم نقطه اعشار دو عدد شرکت کننده در محاسبه باید با یکدیگر تراز شوند. پس تنها در صورتی میتوان عددی با فرمت Uxx08 را با عدد ممیز ثابت دیگری جمع، تفریق و یا تقسیم کرد که عدد دیگر نیز دارای فرمت ممیز ثابت Uxx08 باشد. برای اجرای عملیات ریاضی روی اعدادی که فرمت نمایش متفاوت Uxxyy دارند، ابتدا باید نقطه اعشار دو عدد باهم تراز شوند، هیچ استثنایی هم وجود ندارد.
برای جمع، تفریق یا تقسیم نقطه اعشار دو عدد شرکت کننده در محاسبه باید با یکدیگر تراز شوند.
برای تراز کردن نقطه اعشار اعداد دو انتخاب وجود دارد:
- ضرب عدد بزرگتر در ضریب 2X یا
- تقسیم عدد کوچکتر بر 2X
به بیان سادهتر عدد با تعداد بیت صحیح بیشتر را در 2X و عدد با تعداد بیت صحیح کمتر را در 1/2X ضرب می کنیم.
ضرب
در زمان محاسبه حاصل ضرب دو عدد، نیازی به تراز کردن نقاط اعشار نداریم. زیرا تعداد بیتهای حاصل از ضرب دو عدد با جمع کردن تعداد بیتهای آن دو محاسبه میشود. به بیان سادهتر بیتهای صحیح باهم و بیتهای اعشار باهم جمع میشوند. اگر فرض کنیم x1 و x2 تعدا بیتهای صحیح و y1 و y2 تعداد بیت های اعشاری دو عدد هستند، برای پاسخ داریم: x1 + x2, y1 + y2.
در زمان محاسبه حاصل ضرب دو عدد، نیازی به تراز کردن نقاط اعشار نداریم.






