How to build the real random number!

Building the real random numbers

When you try to build a game, encryption algorithm or other uses you may need to build the random numbers! You may think that it is not complex to make the random numbers or you call the RAND function or similar and then the project will be finished. But how much these numbers are random? Is the result repeatable?

In this article we aim to challenge this subject so follow the Sisoog.

Why cannot random numbers be called really random?

There is no difference which language you are using for the programing; Typically to build random numbers a function is used which produce the random numbers. To prevent of complexity and the result can be testable, C language consider as a reference and examples are written In C language. In C language there is a function which builds random numbers. If we look inside this function there is an algorithm without any variable parameter. For each run of this function, depending on the algorithm a definite result return. To elaborate pay attention below example:

int main(void)
{
	int i = 0;
	for(i=0;i<10;i++)
		printf("%i\t",rand());
}

int main(void)

{

int i = 0;

for(i=0;i<10;i++)

printf("%i\t",rand());

}

In the above code we are going to build 10 random number and demonstrate the result. To do this we use a loop which calls the RAND function 10 times and show the output. The sequence of number produced seems to be random. If we survey the algorithm and its method and find how it works; we can predict the next or previous numbers by having one of the numbers.

41	18467	6334	26500	19169	15724	11478	29358	26962	24464

1	41 18467 6334 26500 19169 15724 11478 29358 26962 24464

We expect to have 10 different number by each running of the RAND function; but if we execute the code each time, we can see all the produced numbers are same with the previous numbers. (It is possible for you to have different numbers but the result is repeatable). This means that the produce numbers are not really random numbers which produced through an algorithm without having a variable parameter. To solve this setback, there is a function which name is SRAND. This function has a variable parameter which receive a number as a setpoint and build the random number from this setpoint. If we give a number in every run of this program the output is randomly. Building this setpoint is another problem. At first the program run there is no any random number as a set point. To have a different result in each run we set the time as a setpoint or entrance of this function. It seems that is reasonable. Every time the program run regarding the time the result is different.

int main(void)
{
	int i = 0;
	srand ( time(NULL) );
	for(i=0;i<10;i++)
		printf("%i\t",rand());
	return 0;
}

int main(void)

{

int i = 0;

srand ( time(NULL) );

for(i=0;i<10;i++)

printf("%i\t",rand());

return 0;

}

In each running of the code, we have divergent results. Compare to the previous method, the result has ameliorated a bit but the problem has not solved completely. The reason it that if the code run in a short time the results will be same and the numbers are not random. The calculation of them just turn difficult. Imagine we founded an encryption random code system base on this method, a hacker by knowing the building time of the codes, can guess the codes and crack the encryption. As you can see the produced numbers are not really random and can predictable but not for everyone.

Why this trend is more deteriorated in microcontroller-based systems?

Generally, microcontroller-based systems do not have the RTC (Real time clock) and the system time normally measure when the device turning on. This issue lead to the SRAND function to be useless practically. The function in the program always is called at specific time and receive a specific number to start. To elaborate on this, we rewrite the above software for Arduino hardware.

void setup() {
  // put your setup code here, to run once:
  Serial.begin(9600);
  srand(millis());

  for(int i=0;i<10;i++)
    Serial.println(rand());
}

void loop() {
  // put your main code here, to run repeatedly:

}

void setup() {

// put your setup code here, to run once:

Serial.begin(9600);

srand(millis());

for(int i=0;i<10;i++)

Serial.println(rand());

}

void loop() {

// put your main code here, to run repeatedly:

}

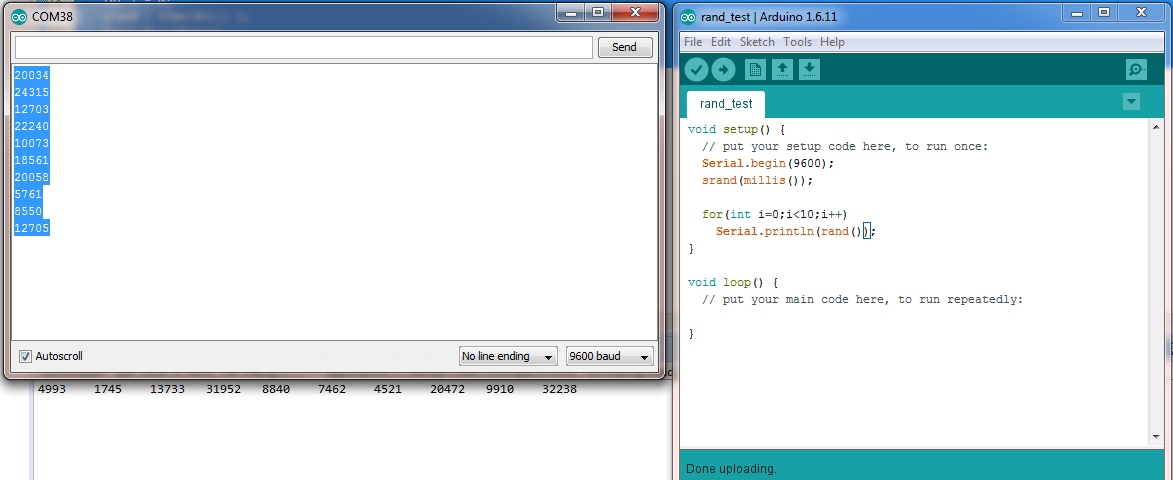
As you can see after any reset or turning on or off the microcontroller, the code has an equal output. We should consider that if use a RTC in system, the condition ameliorated a bit and predicting the output get tough, but they are not real random numbers yet. To have a sequence of real random number, we need two conditions:

First: The sequence should not be repeatable.

Second: The produce numbers should not be conjecturable.

What is the solution for producing the real random numbers?

As, we mentioned above we call the numbers really random when they obey two above conditions. If we consider the agglomeration of a specific bacterium on a surface, the produced number with this method are not conjecturable easily, because there are a lot of factors in growth of bacteria; As an example: temperature and humidity of the weather, intensity of the light, and so on… .For this reason actually it is impossible to guess the amount of bacteria in a specific time so we can say that the numbers are really random. The above example is just show that we can reach real random numbers by increasing the factors which contribute to produce the random numbers. There are numerous ways in producing random number through above methods but the simple methods are limited. In this article we are going to produce the real random numbers by using the White Noise. According to physics scientists the White Noise is a random signal which has a constant spectrum density. To elaborate on this, human ear can responses the frequency district from 20Hz to 20KHz. If a sound device wants to make a White Noise for us, it should have an ability to emit the sound from 20 Hz to 40Hz frequency range and be equal with the power of wave which has the frequency for instance from 10000 Hz to 10020 Hz. Listen to White Noise sound:

The sound of ocean is a type of White Noise:

How to produce a White Noise?

The simplest way is using of a diode in revers bias. As you know the diode contains the junction of N and P. when we put the diode in revers bias, the P-N junction extended and a low amount of current is flown. The name of this is leakage current. Given the quiddity of the diode the P-N junction has White Noise. Base on this we can use below circuit to produce it:

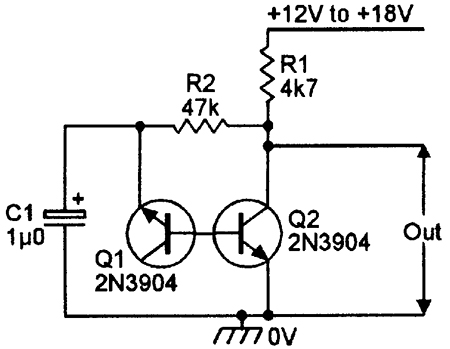
If we connect the output of the circuit to a sound amplifier, we can hear the White Noise. To amplify and rectify the impedance it can connect to an op-amp. This is the final circuit:

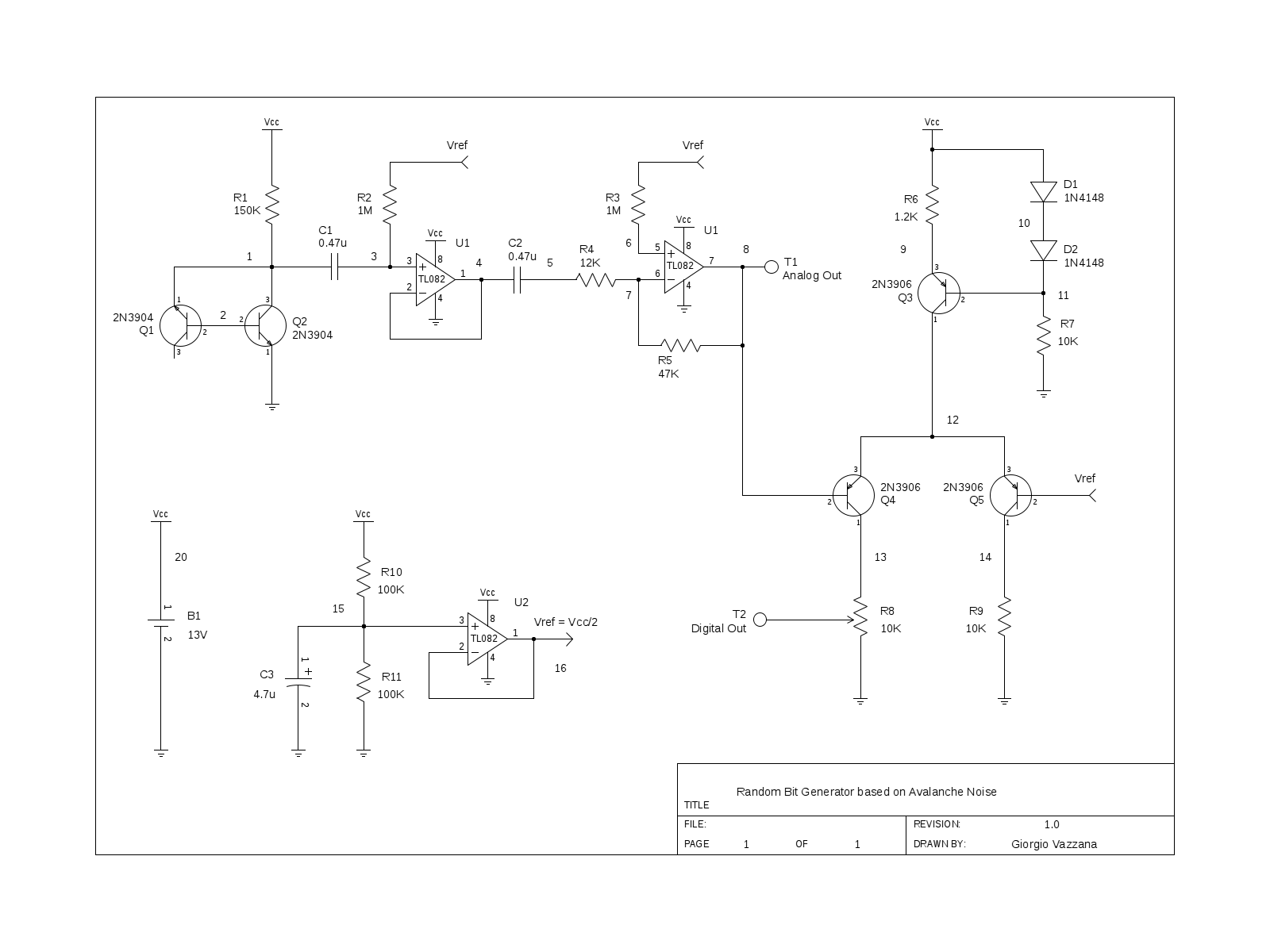
How could I use the White Noise generator?

The above circuit can be connected to the entrance ADC of a microcontroller or a PC sound card! The obtained results are absolutely random and there is no way to repeat the produced numbers. White Noise, ADC, Rand and Srand functions are used in this code to produce random numbers.

int adc_pin = 0;

void setup(){

  Serial.begin(9600); 
}

void loop()
{
  
  int adc_value = analogRead(adc_pin);
  srand(adc_value);
  Serial.println(rand());
  delay(1000);
}

int adc_pin = 0;

void setup(){

Serial.begin(9600);

}

void loop()

{

int adc_value = analogRead(adc_pin);

srand(adc_value);

Serial.println(rand());

delay(1000);

}

Analyzing the results:

We estimated and recorded the output of the generator circuit for 15 hours with 500 micro second sample rate. If consider each bit a one pixel and display the recorded data into a picture, we gain the below picture which is like an old tv snowy screen.

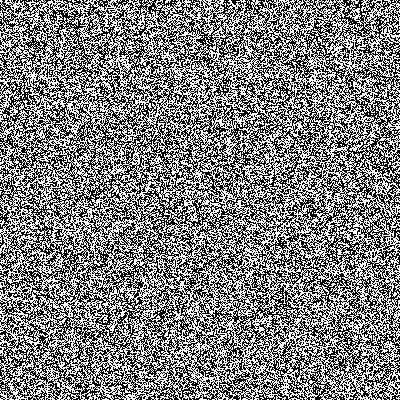
Listen the first 882000 samples as an audio file: