RSA algorithm and the miracle of the prime numbers

During last weeks I was involved with encryption algorithms ranging from symmetric to asymmetric encryption algorithms, it is really complex and amazing world witch all of them are math basis. Already we talked about the importance of producing random numbers in previous article and tried to solve the problem through hardware design. If you want know about this article follow this link How to produce real random numbers?

Random numbers play the fundamental role in producing encryption keys, the more randomize produced numbers, the more complex and unpredictable keys are. Sometimes I saw in articles that they have worked on random numbers producing optimization but, I had never thought about the importance of these numbers! For instance, what is the usage of a primary number like 128? I noticed the importance and beauty of mathematics when I was trying to implement the RSA idea, I did not have a lot of memory and was forced to use prepared library.

In this article we want to demonstrate the principles of RSA algorithm in a simple way so follow the Sisoog and introduce our website to your friends.

When it comes to encryption what are we talking really about?

We talk about the encryption and its usage in modern devices, at first you should know that encryption idea is not new idea and the first encrypted algorithm dated back to 1900 BC. Basically, the aim of encrypting a data is saving or transferring it which just authorized people can identify or decode it.

In the past the most usage of the encryption was in the wars and sensitive government negotiations, the very epitome of which is Enigma which used in second world war. Germans had encrypted the sensitive commercial and military messages through the Enigma and the other side of the war could not understand the messages. We strongly recommend that to watch the Imitation Game movie if you are keen on to know how the Enigma decoded.

But these days considering the privacy and efforts of commercial companies to decode the activities of competing companies and expanding in usage of IOT devices are the examples of using encryption in our daily life.

What is the symmetric and asymmetric encryption?

At the beginning the encrypting and decoding is done by an identical key, it is mean that for the encryption and decoding we need an exclusive key. There are a lot of algorithms which use this principle like AES which is the famous one and XOR which is the simplest one. This method is named as symmetric method.

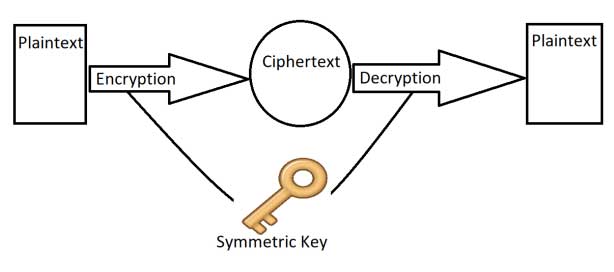
Symmetric encryption algorithm

Although this method is effective, it has serious problems in some applications. If people have the key, they can do encryption and decoding. To prevent eavesdropping and revealing the information, it is vital to carry the key in a safe way and sure that it will not reveal in any way. This issue had a lot of challenge for big company so asymmetric algorithm was suggested.

This is assumption in asymmetric encryption algorithm that the media to carry the information is not safe and each person wants can eavesdrop the data.so definitely we can not use the symmetric method. To solve this problem, we use two keys instead of using one key. In this way the encrypted information through one key just can decoded with another key. With this method we can broadcast the first key witch is nominated public key in unsafe environment without any fear and keep the second key which is nominated private key and then decode the encrypted data.

A brief about the RSA encryption algorithm

There are a lot of algorithm which use the asymmetric key but one of the first to be used is RSA algorithm which is very popular among engineers. This algorithm is the first reliable algorithm among other encryption algorithms of course, can boldly considered it as one of the most important leaps in the field of encryption.

Actually, the RSA is made up of the first three letters of the name of its inventors (Adleman,Ron Rivest,Adi Shamir) which introduced this method in 1977 publicly.

 

Az a matter of fact, RSA is a slow algorithm so never is used for exchange of information. Having the private and public key which enable this algorithm to sharing the public key among users without any worry we can consider this algorithm as a powerful one. Normally a symmetric algorithm is uses for transferring the key.

Let us to elaborate on its functionality give a real scenario as an example, to open a website which is in https format, at first your browser sends a request to a server, the server sends the public keys to your browser, after the browser verification server sends through RSA the key of one of the symmetric encryption algorithms which acceptable by your browser. For instance, the key AES256 and after that all the exchanges between your browser and server is based on the AES symmetric method.

How RSA encryption algorithm does this?

We do not want to show the mathematic theories of RSA algorithm, we try to show simply how it works. We need a scenario an define it as below:

Assume that your browser wants to send number 14 which we label it (P) to a server, the server after receiving the encrypted text decodes it and extract real data. In this example we use the little numbers to enable you to track what happen. In the following we survey the steps for this transaction:

Before any exchanges the server should makes the private and public keys.

• To start the transaction the browser should obtain the public key from the server, this trend usually begins by the browser request.
• In reply server gives the public keys which contain k=7 and n=33 to the browser.
• The browser through the received key encrypts its text P=14 and sends to the server the encrypted text E=20.
• The server receives the encrypted text E=20 and uses its private key J=3 and public key n=33 to extract the real data and decodes this text to main data which is P=14.

Now that we are familiar with the general principles of the RSA algorithm, we will examine the steps in more details.

First stage: making the private and public keys by the server

1. We select two completely prime numbers; it is better these numbers be big. Assume that we have chosen these two numbers: p=3, q=11.

2. By using of these two numbers we calculate the public part of the key, based on selected numbers through below formula the calculated value is 33.

3. Now we can calculate the Z through this formula which based on previous numbers is 20.

4. Now we should choose the prime number K in such a way it is also prime to Z which means that the number Z is not divisible. To elaborate we can choose these numbers 7,11,13,17,19 but we can not choose the 5 because 20 is divisible by 5. We choose the smallest number k=7. (Actually, the bigger number is better but, in this example, we want to mental calculation so the smallest number provide us with smallest calculation).

5. So far, we have created the public key, i.e. n=33 and k=7.

6. Before starting any transaction we should make the private key through below formula:

The value of j, which is actually our private key, is calculated using this relation. We should choose a number as j in addition to being a prime number, is the product of K multiplied by the remainder of Z. in this example we can choose j=3.

So far, we have calculated the public keys and private key. Caution! You should not provide any private keys to the users.

Second stage: encrypting the data in browser

To encrypt the data, we use the below formula, in defined scenario it is supposed to encrypt the P=14 and send it to the server.

In the above formula, the «^» is power operation in mathematics, the n and k are the public keys which received from the server, P means the message that supposed to encrypted and E is the encrypted sentence which is the result of the above formula.

By inserting the calculated numbers, we will finally produce the E=20 which we send it to the server.

Third stage: Decryption of the message on the server

In this stage the server receives the encrypted message from the client and then through the below formula extracts the main message.

• In the above formula <<^>> means power.
• j is the private key
• n is the part of public key
• E is the encrypted message
• P is the message that user sends
• By placing proportional numbers in the above formula, the unencrypted number will be displayed.

Here we do not talk about the back ground theories of the formula, just try to show you the function in a simple way.

Is this possible to hack the RSA algorithm?

The main condition of the RSA algorithm is the dependency between the private and public keys, but it must be hard to find this relation for the stranger from the outside to keep the safety. As you see in the beginning of the article which was about making the keys all things start by making the p and q numbers which we calculated the n through them.

The public key is made of two n and k numbers which the k has made from the z and the z has calculated from the p and q, the private key j is calculated through k and z, as we said k and z is derived from p and q. Therefore, j can be calculated from the p and q which proves that the private and public keys are depended each other.

Therefore, if a foreign person wants to calculate the private key j, needs to decompose the n to two prime numbers which n is made from them, in a way we can say that the strength of this algorithm is here.

If the n is a big number almost impossible to decompose it into two prime numbers which n made from. For this reason, in calculation of the keys use the bigger numbers.

The numbers which need 1024,2048 even 4096-bit memory to save. Imagine a number which demands 2048-bit memory to save and how much is big and how difficult it would be to decompose and how much processing power would be required.

One of the reasons for being slowness of this algorithm is working with this huge numbers which the computer should operates the mathematics function like power and residual on this huge numbers. Increasing difficulty is when we want to find such prime integers for p and q.