آموزش محاسبه سریع لگاریتم در FPGA

در این آموزش می‌خواهیم با یک الگوریتم سریع برای محاسبه تابع لگاریتم که می‌توان به‌راحتی در سیستم‌های دیجیتال مانند FPGA پیاده‌سازی کرد، آشنا شویم. برای پیاده‌سازی این الگوریتم در FPGA به Look Up Table کوچکی نیاز می‌باشد. این روش با سرعت بیشتر و سخت‌افزار کمتر می‌تواند لگاریتم را محاسبه کند.

برای محاسبه لگاریتم میمی‌توانز بسط سری تیلور آن استفاده کرده و چند جمله از آن را محاسبه کنیم. در محاسبه لگاریتم با استفاده از این روش به زمان (تعداد کلاک) و سخت‌افزار بیشتری نیاز است؛ چون محاسبه هر جمله از آن باید تقسیم و به توان رساندن را محاسبه کنیم، همچنین برای افزایش دقت باید جملات بیشتری محاسبه شود.

یک روش دیگر برای محاسبه لگاریتم، استفاده از الگوریتم CORDIC می‌باشد. این روش با استفاده از Look Up Table کوچک قابل‌پیاده‌سازی می‌باشد؛ اما از معایب آن می‌توان به iterative بودن الگوریتم (چند تکرار از الگوریتم باید اجرا شود تا نتیجه به دست آید) اشاره کرد. برای اینکه لگاریتم را با استفاده از الگوریتم CORDIC محاسبه کنیم تعداد کلاک زیادی (برای دقت خوب تقریباً بیشتر از 10 کلاک) باید منتظر بمانیم تا نتیجه محاسبه شود.

روشی که در این مقاله می‌خواهیم برای محاسبه لگاریتم با آن آشنا شویم با سرعت بیشتر (تعداد کلاک کمتر) می‌تواند تقریبی از لگاریتم را محاسبه کند. این روش را می‌توان با استفاده از Look Up Table کوچک پیاده‌سازی کرد. دقت خروجی محدود به سایز جدول Look Up Table می‌باشد. این روش از نمایش نماد علمی عدد استفاده کرده و از روی آن لگاریتم عدد را به‌صورت سریع محاسبه می‌کند لگاریتم در هر پایه‌ای می‌توان از این روش استفاده کرد و روش محدود به لگاریتم در مبنای خاص نمی‌باشد و مقدار مبنا، مقادیری که باید در جدول Look Up Table ذخیره شوند را تعیین می‌کند.

روشی که در این مقاله می‌خواهیم برای محاسبه لگاریتم با آن آشنا شویم با سرعت بیشتر (تعداد کلاک کمتر) می‌تواند تقریبی از لگاریتم را محاسبه کند. این روش را می‌توان با استفاده از Look Up Table کوچک پیاده‌سازی کرد. دقت خروجی محدود به سایز جدول Look Up Table می‌باشد. این روش از نمایش نماد علمی عدد استفاده کرده و از روی آن لگاریتم عدد را به‌صورت سریع محاسبه می‌کند لگاریتم در هر پایه‌ای می‌توان از این روش استفاده کرد و روش محدود به لگاریتم در مبنای خاص نمی‌باشد و مقدار مبنا، مقادیری که باید در جدول Look Up Table ذخیره شوند را تعیین می‌کند.

در نمایش عدد به‌صورت نماد علمی، عدد را به‌صورت حاصل‌ضرب یک عدد اعشاری که قسمت صحیح آن تک‌رقمی می‌باشد ضرب در توان صحیحی از مبنای عدد می‌نویسیم. برای مثال عدد 249. 5 را که در مبنای 10 می‌باشد نمایش نماد علمی این عدد برابر است با:

2.4925 * 10^2  که به‌صورت2.4925e+2 هم نمایش داده می‌شود.

ممیز را چنان جابه‌جا می‌کنیم که در قسمت صحیح (سمت چپ ممیز) فقط یک عدد (یک رقم غیرصفر) باقی بماند. عدد به‌دست‌آمده را در مبنا به توان تعداد جابه‌جایی ضرب می‌کنیم. جابه‌جایی ممیز اگر به سمت چپ باشد علامت توان مبنا مثبت و اگر جابه‌جایی ممیز به سمت راست باشد علامت توان مبنا منفی می‌شود. در مثال بالا عدد در مبنای 10 است و ممیز2  رقم به سمت چپ حرکت کرده است؛ بنابراین توان مبنا +2 می‌شود.

مثال دیگر:

0.0000712 = 7.12 * 10^-5 = 7.12e-5

به توان مبنا Exponent گفته می‌شود.

در مبنای 2 هم می‌توان اعداد را به‌صورت نماد علمی نمایش داد که در سیستم‌های دیجیتال در فرمت ممیز شناور (Floating Point) از نمایش عدد به‌صورت نماد علمی استفاده می‌کند و علامت، Exponent و Mantissa در حافظه ذخیره می‌شود.

ابتدا معادل باینری عدد 49.25 را به‌دست می‌آوریم.

می‌خواهیم این عدد که در مبنای 2  می باشد را به صورت نماد علمی نمایش دهیم. مشابه قبل ممیز را جابجا می‌کنیم که فقط یک رقم در قسمت صحیح باقی بماند. سپس عدد را در 2 به توان تعداد جابجایی ممیز ضرب می‌کنیم.

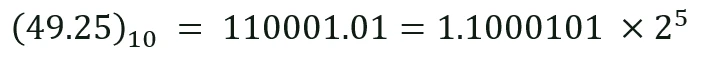
تنها رقم دودویی که می‌تواند در قسمت صحیح در نمایش عدد به‌صورت نماد علمی قرار بگیرد، رقم 1 باینری است (در مبنای2 تنها رقم غیر صفر، رقم یک می باشد). چون به غیر از حالت های خاص (مانند عدد صفر) این مقدار ثابت بوده و باید مقدار آن برابر با 1 باشد. در نگهداری اعداد به فرمت ممیز شناور (floating point) این رقم در حافظه ذخیره نمی‌شود و به آن hidden bit یا hidden integer bit گفته می‌شود (تک بیت صحیحی که می‌دانیم مقدار آن برابر با 1 است، به غیر حالت‌های خاص).

اعداد باینری بدون علامت (مثبت) را در فرم نماد علمی می‌توان به‌صورت 1.M*2^E نشان داد که E همان Exponent بوده و M بیت‌های مربوط به قسمت اعشاری بعد از ممیز می‌باشد.

لگاریتم عدد x = 1.M*2^E را به‌صورت زیر محاسبه می‌کنیم:

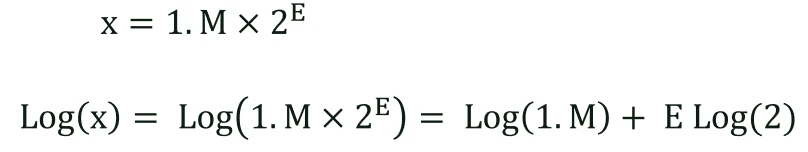
M مربوط به قسمت بعد از ممیز می‌باشد؛ بنابراین مقدار آن کمتر از 1 می‌باشد؛ ازاین‌رو عدد 1.M در بازه‌ی 1<= 1.M < 2 قرار می‌گیرد و لگاریتم آن در بازه Log(1) <= Log(1.M) < Log(2) قرار می‌گیرد.

لگاریتم عدد x را می‌توان با جمله‌ی E*Log(2) تقریب زد به طور تقریبی لگاریتم عدد را به‌صورت Exponent ضرب در Log(2) محاسبه کرد. در مثال زیر مقدار دقیق و تقریبی لگاریتم چند مقدار را محاسبه می‌کنیم.

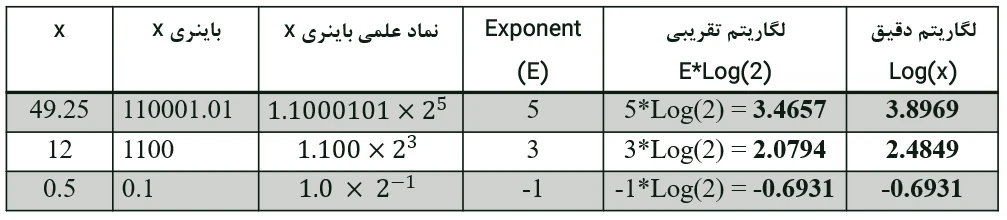
مقدار Exponent در واقع محل اولین بیت 1 پرارزش می‌باشد. برای مثال در معادل باینری عدد 49.75 پرارزش‌ترین بیت 1 در محل بیت 5 در قسمت صحیح قرار دارد (ارزش این بیت 2^5  می‌باشد) که برابر با همان مقدار Exponent این عدد در حالت نمایش به‌صورت نماد علمی می‌باشد. ازاین‌رو برای محاسبه لگاریتم به‌صورت سریع در سیستم‌های دیجیتال برای مثال FPGAها می‌توان محل پرارزش‌ترین 1 را در عدد پیدا کرده و سپس آن را در Log(2) ضرب کنیم و تقریبی از لگاریتم عدد را به دست آوریم. برای اینکه هر بار نیاز به محاسبه‌ی ضرب نباشد هم می‌توان از یک جدول حافظه Look Up Table (LUT) استفاده کرد.

اعداد را در سیستم‌های دیجیتال با تعداد بیت محدود نگهداری می‌کنیم؛ لذا برای محاسبه تقریبی لگاریتم به روش بالا، می‌توانیم از یک جدول حافظه یا Look Up Table استفاده کنیم و بدون اینکه نیاز به ضرب‌کردن باشد خروجی را محاسبه کنیم. تعداد بیت‌ها که محدود و مشخص می‌باشد، بیت 1 پرارزش در هر یک از این محل‌ها می‌تواند قرار بگیرید؛ بنابراین در یکLUT به طول تعداد بیت‌ها می‌توانیم مقدار حاصل ضرب Exponent در Log(2) را نگهداری کنیم با این کار دیگر نیاز نیست که هربار این حاصل ضرب را محاسبه کنیم. برای محاسبه ی لگاریتم ورودی ابتدا از یک انکدر الویت دار استفاده کنیم تا محل اولین بیت 1 پرارزش ورودی یا به عبارت دیگر مقدار Exponent را پیدا کنیم و سپس از روی خروجی انکدر الویت دار به عنوان آدرس LUT استفاده کرده و محتوای موجود در آدرس Exponent از LUT را که مقدار E*Log(2) در آن قرار دارد و تقریبی از مقدار لگاریتم ورودی می باشد را در خروجی قرار دهیم.

بهبود دقت خروجی

مقدار لگاریتم x برابر است با Log(1.M) + E*Log(2) که در بالا آن را فقط با جمله‌ی E*Log(2) تقریب زدیم. برای محاسبه لگاریتم ورودی با دقت بهتر می‌توانیم از M هم استفاده کرده و مقدار جمله‌ی Log(1. ) را به مقدار تقریبی لگاریتم که از روی Exponent به‌دست می‌آوریم اضافه کنیم. برای اینکار می توان قسمت اعشاری یا همان M را با چند بیت تقریب بزنیم یا به عبارت دیگر از چند بیت پر ارزش آن استفاده کنیم تا تقریبی از Log(1. ) را محاسبه کنیم. این قسمت را می‌توانیم با استفاده از یک LUT کوچک پیاده‌سازی کنیم که از بیت‌های پرارزش M برای انتخاب آدرس LUT استفاده کرده و در آن آدرس‌های حافظه مقدار تقریبی Log(1. ) را ذخیره کنیم. هرچقدر تعداد بیت بیشتری از M را در نظر بگیریم با دقت بالاتری جمله‌ی Log(1. ) را می‌توانیم محاسبه کنیم. با استفاده‎ کردن از 4 بیت پرارزش M می توان به دقت خوبی دست پیدا کرد.

برای مثال اگر از 4 بیت پرارزش M بخواهیم استفاده کنیم، 4 بیت 16 مقدار مختلف می‎تواند داشته باشد. مقدار لگاریتم این 16 عدد را که از 1.0000 تا 1.1111 می‎‎‌شود را محاسبه کرده و در یک LUT ذخیره می‌کنیم. برای محاسبه‌ی جمله‌ی Log(1. ) از 4 بیت پرارزش M استفاده می‌کنیم و تقریبی از این جمله را به‌دست می‌آوریم. اسم این LUT را Mantissa LUT در نظر می‌گیریم.

در این حالت هم مشابه قبل هنگامی که می‌خواهیم لگاریتم ورودی را محاسبه کنیم ابتدا باید محل پرارزش‌ترین بیت 1 (Exponent) را به‌دست آوریم سپس از روی محل به‌دست‌آمده و LUT مربوط به قسمت Exponent مقدار E*Log(2) را به دست می‌آوریم. بعد از محل پرارزش‌ترین بیت 1 (پایین تر از ممیز، سمت راست ممیز) قسمت M می باشد. از قسمت M ،4 بیت پرارزش را انتخاب می‌کنیم (در این مثال فرض کردیم از 4 بیت M می‌خواهیم استفاده کنیم) و از این مقدار به عنوان آدرس Mantissa LUT استفاده می‌کنیم و این آدرس از Mantissa LUT را انتخاب می‌کنیم. می‌دانیم در آدرس انتخابی مقدار لگاریتم یک ممیز 4 بیت بعد از آن قرار دارد (تقریب 4 بیت اعشار جمله Log(1.M)). در آخر مقدار به‌دست آمده از Exponent LUT را با مقدار به‌دست آمده از Mantissa LUT جمع کرده و تقریب بهتری از لگاریتم ورودی را محاسبه می‌کنیم.

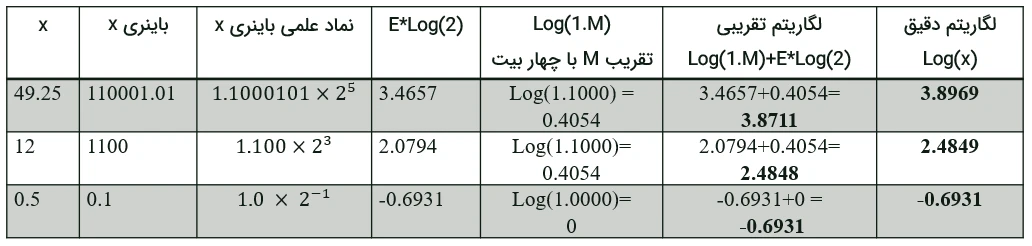
می‌توان مشاهده کرد که روش با دقت بالاتری مقدار لگاریتم را محاسبه می‌کند.

در این آموزش یاد گرفتیم که چطور می‌توانیم لگاریتم را به‌صورت تقریبی و با سرعت بالا در سیستم‌های دیجیتال پیاده‌سازی کنیم.

منبع:

http://dspguru.com/dsp/tricks/quick-and-dirty-logarithms/