آموزش محاسبه سریع لگاریتم در FPGA _ قسمت سوم (پیاده‌سازی - افزایش دقت خروجی)

در قسمت اول آموزش دیدیم که اگر بیایم و عدد رو به‌صورت نماد علمی بنویسیم، لگاریتم آن برابر با Log(1.M)+E*Log(2) می‌شود و می‌توانیم برای محاسبه تقریبی مقدار لگاریتم عبارت E*Log(2) را محاسبه کنیم. در قسمت دوم مدار دیجیتالی با استفاده از VHDL طراحی کردیم که عبارت E*Log(2) (تقریبی از لگاریتم) را محاسبه  کند. در این قسمت می‌خواهیم مقدار لگاریتم را با دقت بیشتری محاسبه کنیم.

محاسبه لگاریتم با دقت بیشتر

برای اینکه مقدار لگاریتم را با دقت بیشتری محاسبه کنیم، می‌توان از M هم استفاده کرده و مقدار جمله‌ی Log(1.M) را به مقدار تقریبی لگاریتم که از روی Exponent به دست می‌آید اضافه کنیم. برای پیاده‌سازی این قسمت باید تصمیم بگیریم که مقدار 1.M را با چند بیت اعشار تقریب بزنیم. هرچقدر تعداد بیت بیشتری از M (قسمت اعشاری)  را در نظر بگیریم به حجم حافظه‌ی بیشتر (LUT بزرگ‌تر) نیاز خواهیم داشت.

اگر قسمت اعشاری را با 4 بیت تقریب بزنیم، با دقت خوبی می‌توانیم خروجی را محاسبه کنیم. در این آموزش پیاده سازی را با فرض تقریب 4 بیت M انجام می دهیم. چهار بیت پر ارزش M یا به عبارت دیگر 4 بیت پس از ممیز را m می‌نامیم. اگر بخواهیم M را با 4 بیت پرارزش آن تقریب بزنیم (m)، این مقدار 2 به توان 4 حالت مختلف می‌تواند داشته باشد. مقدار m که فرض کردیم 4 بیتی هست، می‌تواند شامل مقادیر 0000 تا 1111 باشد ( 2 به توان 4 یا همان 16 حالت).

در قسمت اول آموزش برای محاسبه لگاریتم به صورت سریع از نمایش نماد علمی آن استفاده کردیم. در نمایش نماد علمی عدد به این موضوع اشاره کردیم که باید عدد را به صورت یک بیت صحیح، ممیز بیت های اعشار ضرب در 2 به توان Exponent بنویسیم، که مقدار تک بیت صحیح باید برابر با 1 باشد (تنها مقدار غیر صفر در اعداد باینری، 1 می باشد). بنابراین در جمله Log(1.M)، بیت 1 صحیح ثابت هست و فقط M تغییر می کند. همانطور که اشاره کردیم می‌خواهیم مقدار 1.M را با 4 بیت اعشار (1.m) تقریب بزنیم که در این صورت همه‌ی حالت‌های ممکن برابر با 1.000 تا 1.1111 می‌شود.

برای محاسبه‌ی مقدار تقریبی عبارت Log(1.M)، مقدار لگاریتم اعداد 1.0000 تا 1.1111 را محاسبه کرده و در یک LUT ذخیره می‌کنیم و از m به عنوان آدرس LUT استفاده کرده و مقدار Log(1.m) را بدست می آوریم.

محاسبه‌ی مقادیر LUT

با استفاده از برنامه‌ی پایتون زیر، مقادیر جدول Mantissa را محاسبه می‌کنیم. ابتدا همه حالت‌های m را در نظر گرفته سپس مقدار لگاریتم 1.mها را محاسبه می‌کنیم. اعداد به‌دست‌آمده در فرمت floating point می‌باشند؛ برای همین باید آن‌ها را به فرمت ممیز ثابتی که در نظر گرفته‌ایم تبدیل کنیم (اعداد 16 بیتی با 6 بیت اعشار). نتیجه‌ی به‌دست‌آمده را به مقیاس ضرب کرده و پس از گرد کردن به integer تبدیل می‌کنیم تا مقادیر LUT را در فرمت ممیز ثابت موردنظر به دست آوریم.

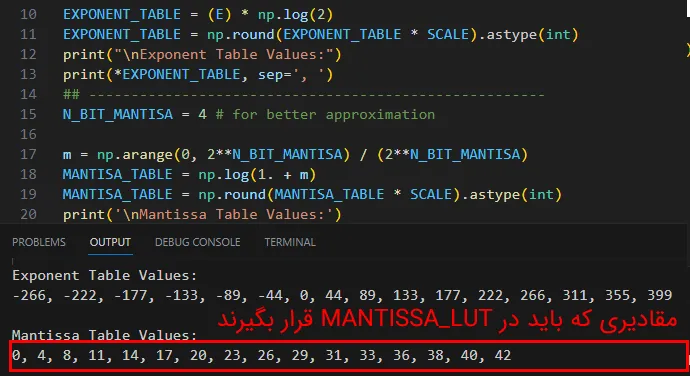
پیاده‌سازی

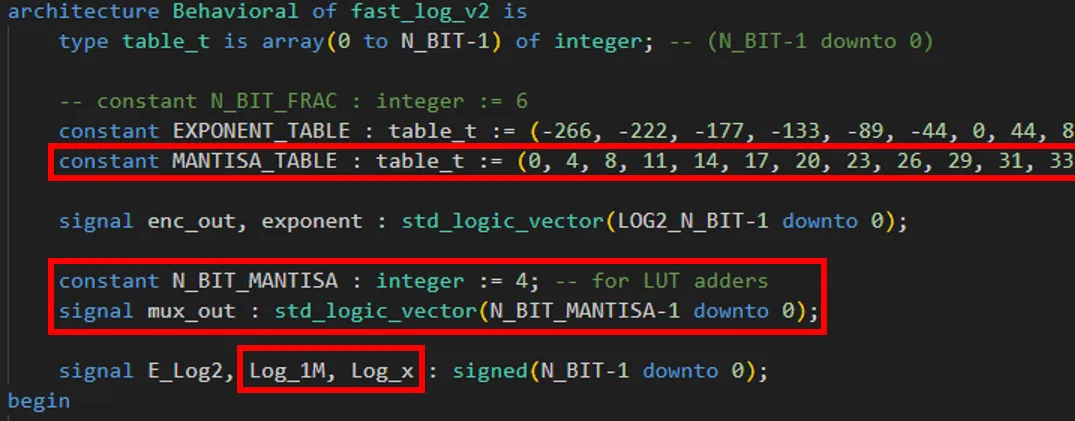
در فایل vhdl قبل از begin قسمت architecture، ثابت MANTISSA_TABLE را از نوع table_t تعریف کرده و مقادیر جدول Mantissa که به دست آوردیم را در آن قرار می‌دهیم.

برای اینکه مقدار تقریبی لگاریتم را محاسبه کنیم در قسمت قبل، از یک انکدر الویت دار استفاده کردیم تا موقعیت پرارزش‌ترین بیت 1 را به دست آوریم. پس پرارزش‌ترین بیت 1 باید مقدار m را به دست آوریم (تقریب 4 بیتی قسمت اعشار یا همان M). برای به‌دست‌آوردن مقدار m از یک مالتی‌پلکسر استفاده می‌کنیم که سیگنال انتخاب آن را موقعیت پرارزش‌ترین بیت 1 یا همان Exponent کنترل می‌کند.

مالتی‌پلکسر سیگنال انتخاب exponent را به‌عنوان ورودی دریافت کرده و در خروجی 4 بیت پس از موقعیت پرارزش ترین بیت 1 را قرار می‌دهد. برای مثال زمانی که مقدار exponent برابر با 15 ( “1111” باینری 15) باشد، پرارزش ترین بیت یک در بیت 15 قرار دارد بنابراین m برابر خواهد بود با بیت‌ها 14 تا 11 مقدار ورودی (4 بیت بعد از 1 پر ارزش). مثال دیگر: زمانی که مقدار exponent برابر با 8 ( “1000” باینری 8) باشد، پرارزش‌ترین بیت یک در بیت 8 قرار دارد بنابراین m برابر خواهد بود با بیت ها 7 تا 4 مقدار ورودی.

اگر مقدار exponent برابر با 2 ( “0010” باینری 2) باشد، پس از آن فقط بیت های 1 و 0 وجود دارد (فقط دو بیت وجود دارد) ولی ما به مقدار m چهار بیتی نیاز داریم. بیت های پس از پرارزش‌ترین بیت 1 مربوط به قسمت اعشاری می‌باشد، بنابراین زمانی که تعداد بیت های پس از آن کمتر از 4 بیت باشد، از سمت راست به آن 0 اضافه می کنیم تا طول آن برابر با 4 بیت شود.

مالتی‌پلکسر را با with select پیاده‌سازی می‌کنیم. سیگنال انتخاب را مقدار رجیستر exponent در نظر می‌گیریم.

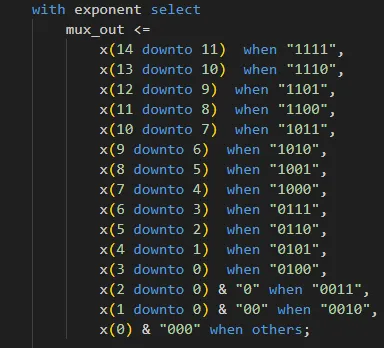
از کد پایتون زیر می‌توانید برای تولید کد VHDL مالتی‌پلکسر استفاده کنید.

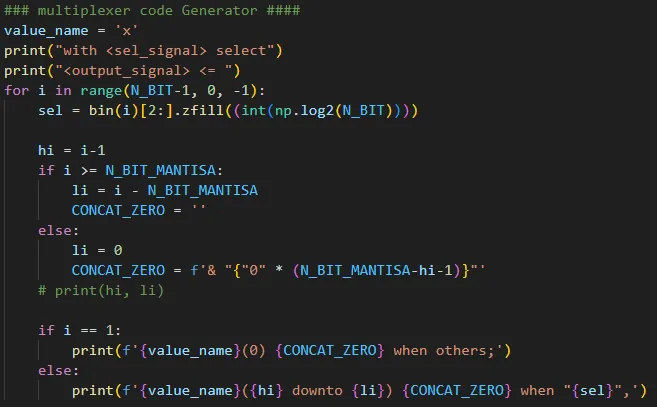
با استفاده از مالتی‌پلکسر مقدار m را به دست می‌آوریم. پس از به‌دست‌آوردن m، برای محاسبه‌ی مقدار Log(1.m) کافی‌ست از جدول Mantissa آدرس m (اندیس m) را انتخاب کرده و از مقدار آن استفاده کنیم.

خروجی مالتی‌پلکسر (mux_out) از نوع std_logic_vector می‌باشد. برای اینکه از mux_out که از نوع std_logic_vector هست به‌عنوان اندیس استفاده کنیم ابتدا آن را به unsigned و سپس به integer به‌صورت زیر تبدیل می‌کنیم:

سپس این اندیس از LUT را به‌صورت زیر انتخاب می‌کنیم:

مقادیری که در هر آدرس از جدول قرار گرفته‌اند، مقدار Log(1.m) در فرمت Fixed Point  می‌باشد. با انتخاب این اندیس از جدول، مقدار تقریبی Log(1.M) را به دست می‌آوریم. مقادیر موجود در آرایه از نوع integer  می‌باشند. خروجی آرایه را با استفاده از تابع to_signed به عدد علامت‌دار 16 بیتی تبدیل می‌کنیم و نتیجه را در رجیستر 16 بیتی Log_1M ذخیره می‌کنیم.

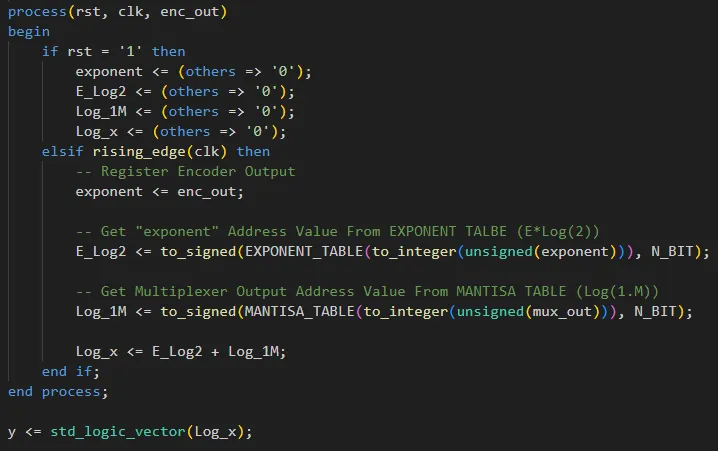
رجیستر کردن خروجی LUT در رجیستر Log_1M را در هر لبه‌ی بالارونده‌ی کلاک انجام می‌دهیم.

زمانی که در ورودی مقدار موردنظر قرار می‌گیرد، در کلاک اول خروجی انکدر اولویت‌دار در exponent رجیستر می‌شود. در کلاک بعدی مقدار E*Log(2) در رجیستر E_Log2 و مقدار Log(1.m) در رجیستر Log_1M قرار می‌گیرد. در کلاک بعد مقدار این دو رجیستر را با هم جمع کرده و در رجیستر Log_x قرار می‌دهیم. به‌این‌ترتیب مقدار لگاریتم ورودی را با دقت بهتری محاسبه می‌کنیم. در خارج از process سیگنال Log_x را به std_logic_vector تبدیل کرده و به y خروجی ماژول وصل می‌کنیم.

سه کلاک طول می‌کشد تا خروجی محاسبه شود. پیاده‌سازی به‌صورت پایپ لاین می‌باشد؛ برای همین می‌توان در هر کلاک مقدار جدید در ورودی قرار داد. در خروجی پس از تأخیر ثابت لگاریتم ورودی‌ها به ترتیب محاسبه می‌شود.

تست بنچ

برای ماژولی که پیاده‌سازی کردیم یک تست بنچ (Test Bench) نوشته و عملکرد آن را بررسی می‌کنیم. از همان تست بنچی که در قسمت دوم آموزش نوشتیم استفاده می‌کنیم.

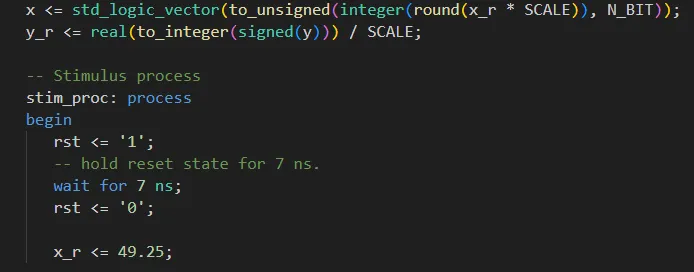
در داخل process شبیه‌سازی ابتدا مدار را ریست کرده (rst=1) و پس از تأخیر کوتاهی از حالت ریست در می‌آوریم (rst=0). پس از ریست‌کردن مدار مقدار ورودی موردنظر 49.25 را در سیگنال کمکی x_r قرار می‌دهیم و شبیه سازی را اجرا می‌کنیم.

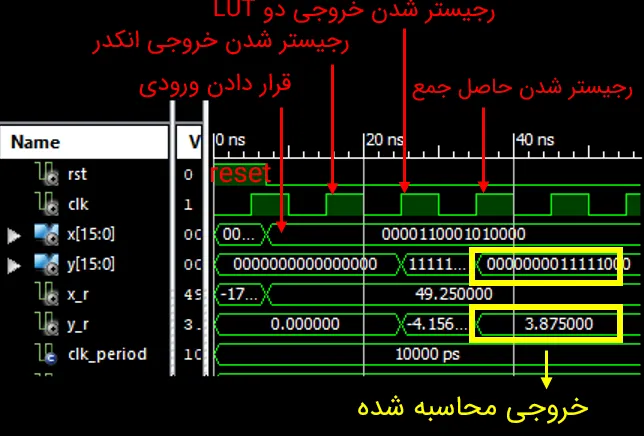
خروجی شبیه‌سازی به‌ازای ورودی 49.25:

پیاده‌سازی که انجام داده‌ایم به‌صورت پایپ لاین می‌باشد و این امکان را فراهم می‌کند که در هر کلاک به ماژول ورودی ارسال کنیم. در تست بنچ پس از اینکه مقدار اول را در ورودی قرار دادیم یک کلاک صبر کرده و مقدار جدید را در ورودی قرار می‌دهیم.

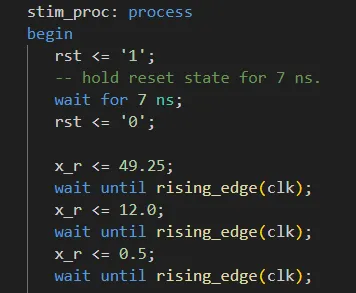
خروجی شبیه‌سازی:

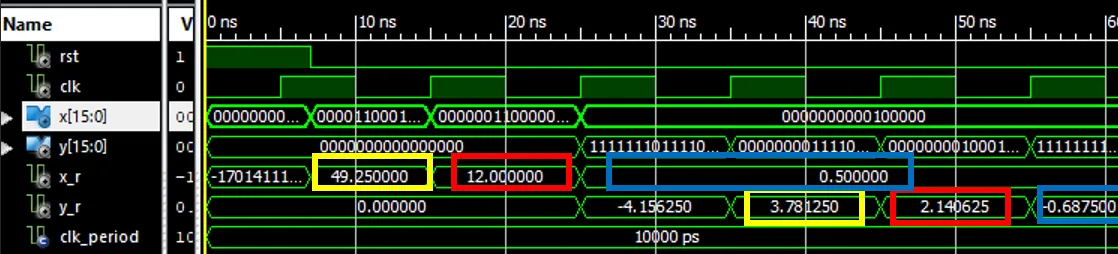
در این قسمت توانستیم با استفاده از با استفاده از LUT برای قسمت Exponent و LUT برای قسمت Mantissa مقدار لگاریتم را با دقت بیشتری محاسبه کنیم.

برای اینکه مقدار لگاریتم را در پایه‌های دیگر (برای مثال 2 یا 10) محاسبه کنیم، کافی‌ست هنگام محاسبه‌ی مقادیر LUTها، از لگاریتم با پایه‌ی مورد نظر استفاده می‌کنیم. با تغییر مقادیر موجود در LUTها، لگاریتم در پایه‌ی موردنظر را می‌توان محاسبه کرد.

فایل‌های این آموزش را می‌توانید از لینک گیت‌هاب زیر دانلود نمایید:

https://github.com/sphrk/Fast_Logarithm_Calculation