آموزش فیلترینگ سیگنال در پایتون | طراحی فیلتر ایده‌آل در حوزه فرکانس (FFT)

در قسمت قبل با آستانه‌گذاری و محدودکردن دامنه سیگنال با روش‌های مبتنی بر indexing آرایه آشنا شدیم. در این قسمت از آموزش می‌خواهیم با استفاده از indexing آرایه فیلترکردن ایده‌آل را در حوزه فرکانس پیاده‌سازی کنیم. در این آموزش فیلتر پایین گذر و میان‌گذر ایده‌آل را در حوزه فرکانس پیاده‌سازی می‌کنیم.

کدهای پایتون نوشته در این آموزش، در یک فایل ژوپیتر نوت‌بوک نوشته شده‌اند. لینک دانلود فایل ژوپیتر نوت‌بوک مربوط به این آموزش در انتهای صفحه قرار داده شده است.

برای تعریف آرایه‌ها کتابخانه numpy و برای ترسیم نمودار کتابخانه matplotlib را import می‌کنیم.

سه سیگنال سینوسی با فرکانس 20 هرتز با دامنه 1 ، فرکانس 130 هرتز با دامنه 1 و فرکانس 200 هرتز با دامنه 0.5  تعریف می‌کنیم و هر سه را با هم جمع کرده و سیگنال x را بدست می‌آوریم. نمودار x را در زمان رسم می‌کنیم.

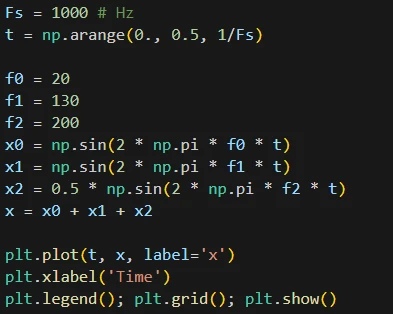
نمودار خروجی:

ترسیم طیف سیگنال در حوزه‌ی فرکانس

برای به‌دست‌آوردن طیف سیگنال در حوزه‌ی فرکانس از تابع fft از کتابخانه numpy استفاده می‌کنیم. این تابع خروجی را در بازه‌ی صفر تا 2*pi (فرکانس گسسته) که معادل است با بازه‌ی صفر تا Fs هرتز (فرکانس پیوسته) تولید می‌کند (Fs نرخ نمونه‌برداری). برای به‌دست‌آوردن دامنه طیف، از تابع abs استفاده کرده و اندازه مقادیر مختلط به‌دست‌آمده را محاسبه می‌کنیم.

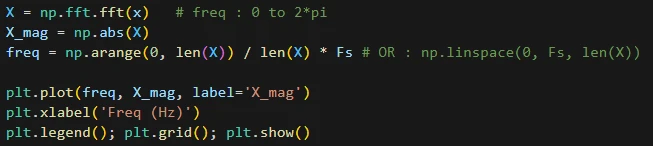
نمودار خروجی:

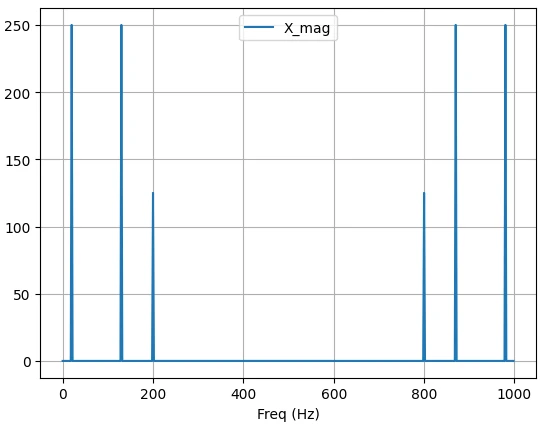
به بازه‌ی صفر تا 500 (Fs/2=500) اگر نگاه کنیم، می‌توان مشاهده کرد در فرکانس‌های 20، 130 و 200 هرتز مقدار دامنه طیف دارای مؤلفه‌ی غیرصفر می‌باشد (همان فرکانس‌هایی هستند که در سیگنال x حضور دارند).

برای به‌دست‌آوردن طیف متقارن می‌توان از fftshift استفاده کرد. این تابع جای نیمه‌ی دوم طیف را با نیمه‌ی اول جابه‌جا می‌کند. پس از اینکه fft سیگنال را به دست آوردیم با اعمال fftshift، طیف در بازه‌ی متقارن -pi تا pi یا به‌عبارت‌دیگر در بازه‌ی -Fs/2 تا Fs/2 قرار می‌گیرد.

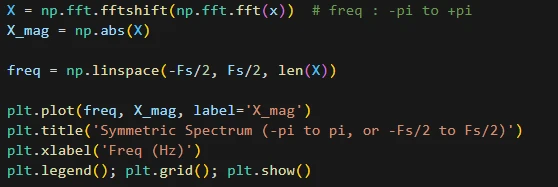
نمودار خروجی:

طیف در بازه‌ی متقارن رسم شده است.

فیلتر پایین گذر ایده‌آل

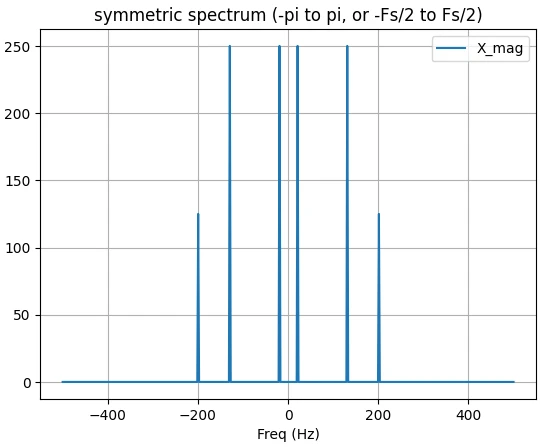
برای تعریف فیلتر پایین گذر ایده‌آل با فرکانس قطع 50 هرتز، از آرایه‌ی فرکانس استفاده می‌کنیم. قدرمطلق فرکانس‌ها را با فرکانس قطع مقایسه می‌کنیم. در آرایه‌ی lpf در جاهایی که قدرمطلق فرکانس از فرکانس قطع کمتر باشد مقدار True (ناحیه‌ی عبور فیلتر) و در بقیه فرکانس‌ها مقدار False (ناحیه‌ی قطع فیلتر) قرار می‌گیرد.

نمودار طیف x و فیلتر پایین گذر ایده‌آل که تعریف کردیم را رسم می‌کنیم.

نمودار خروجی:

می‌توان مشاهده کرد دامنه‌ی طیف فیلتر در بازه‌ی -50 تا 50 هرتز برابر با 1 بوده (ناحیه‌ی عبور) و در بقیه‌ی فرکانس‌ها دامنه صفر است (ناحیه‌ی قطع).

برای اینکه سیگنال x را در حوزه‌ی فرکانس فیلتر کنیم، طیف سیگنال را به طیف فیلتر پایین گذر ضرب می‌کنیم (توجه داشته باشید طیف فیلتر را متقارن در نظر گرفته‌ایم به همین خاطر آن را به طیف متقارن x ضرب می‌کنیم).

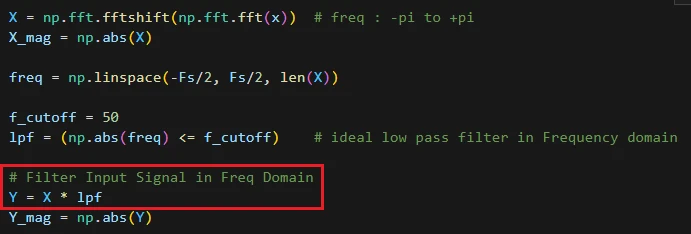
طیف حاصل را در Y قرار داده و دامنه‌ی آن را محاسبه کرده و نمودار آن را رسم می‌کنیم.

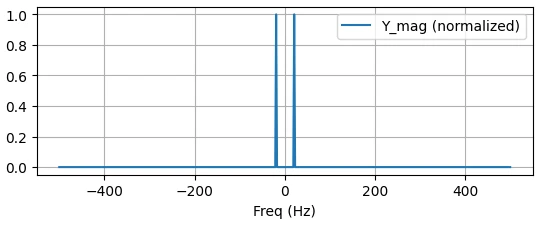
می‌توان مشاهده کرد پس از فیلترکردن، فقط فرکانس 20 هرتز در سیگنال باقی مانده است و دو سینوسی با فرکانس های 130 و 200 هرتز حذف شده اند.

برای به‌دست‌آوردن معادل سیگنال فیلتر شده در حوزه‌ی زمان، ifft (fft معکوس) طیف را محاسبه می‌کنیم. توجه داشته باشید ازآنجایی‌که پس از محاسبه‌ی طیف از fftshift برای به‌دست‌آوردن طیف متقارن استفاده کرده‌ایم، قبل از محاسبه‌ی ifft بایستی طیف را با استفاده از ifftshift (fftshift معکوس) به حالت اول برگردانیم و سپس ifft را محاسبه کنیم.

چون می‌دانیم سیگنال ما حقیقی هست پس از محاسبه‌ی ifft قسمت real سیگنال به‌دست‌آمده را انتخاب می‌کنیم.

نمودار سیگنال y را رسم می‌کنیم.

نمودار خروجی:

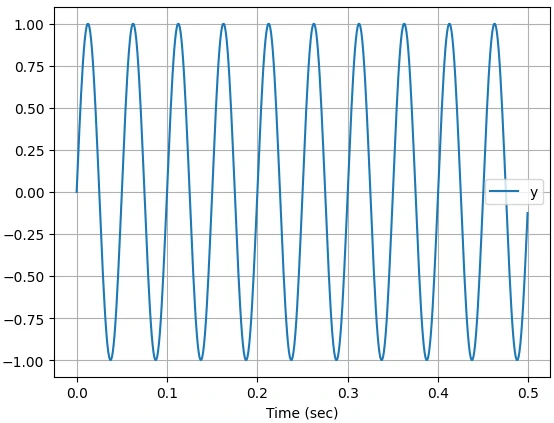
یک سینوسی با فرکانس 20  هرتز رسم شده است (دو نوسان سیگنال 0.1 ثانیه است آنگاه فرکانس سیگنال برابر است با 2 / 0.1 = 20 Hz).

فیلتر میان‌گذر ایده‌آل

می‌خواهیم یک فیلتر میان‌گذر ایجاد کنیم که ناحیه‌ی عبور آن از 100 تا 150 هرتز باشد. برای تعریف فیلتر میان‌گذر کافی‌ست نتیجه‌ی دو آستانه‌گذاری را با یکدیگر and کنیم. فرکانس‌های بزرگ‌تر از فرکانس قطع پایین را انتخاب کرده و آرایه Boolean به‌دست‌آمده را با فرکانس‌هایی که از فرکانس قطع بالا کوچک‌تر هستند and می‌کنیم. به این صورت فرکانس‌های بین فرکانس قطع پایین تا بالا را انتخاب کرده و طیف فیلتر میان‌گذر ایده‌آل را به دست می‌آوریم.

مشابه قبل برای فیلترکردن سیگنال در حوزه‌ی فرکانس، طیف سیگنال را به طیف فیلتر ضرب می‌کنیم. توجه داشته باشید هر دو طیف باید در یک فرمت باشند. در این مثال طیف سیگنال را به‌صورت متقارن در نظر گرفته و از روی آرایه‌ی فرکانس متقارن، طیف متقارن فیلتر را تعریف می‌کنیم. طیف فیلتر شده را در Y قرار داده و دامنه‌ی آن را محاسبه و رسم می‌کنیم.

نمودار خروجی:

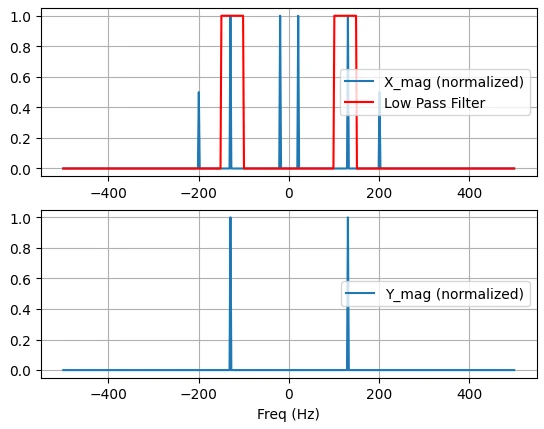
می‌توان مشاهده کرد در خروجی فقط فرکانس 130 هرتز  باقی مانده است.

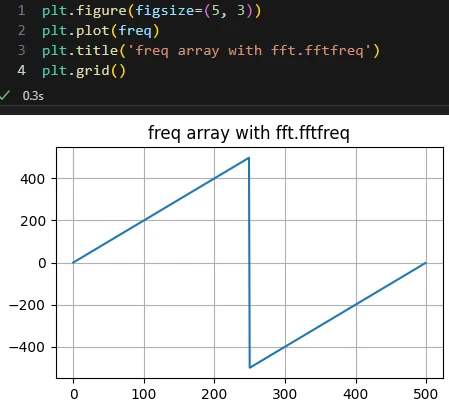
تعریف آرایه فرکانس با fftfreq

موقع ترسیم طیف معمولاً آن را به‌صورت متقارن رسم می‌کنیم. برای به‌دست‌آوردن طیف متقارن در مثال‌های قبلی از fftshift استفاده کردیم. این تابع جای نیمه‌ی اول طیف را با نیمه‌ی دوم آن جابه‌جا می‌کند. با جابه‌جایی که انجام می‌دهد مقادیر طیف به‌صورت بازه‌ی متقارن -pi تا pi در آرایه قرار می‌گیرند. ازاین‌رو آرایه فرکانس‌های متناظر با مقادیر را از  -pi تا pi (یا -Fs/2 تا Fs/2) تعریف می‌کنیم.

وقتی که از fftshift استفاده می‌کنیم، موقع محاسبه‌ی ifft (برگشت به حوزه زمان) حتماً باید توجه داشته باشیم که طیف را به حالت اولیه در بیاوریم، عکس کار fftshift را انجام دهیم با استفاده از ifftshif و پس از آن ifft را محاسبه کنیم. در این حالت مقادیر موجود در آرایه را دو بار جابه‌جا می‌کنیم. برای اینکه بدون جابه‌جایی مقادیر در آرایه، پردازش موردنظر را انجام دهیم می‌توانیم آرایه‌ی فرکانس‌ها را به‌صورت هوشمندانه تعریف کنیم.

موقع ساخت آرایه‌ی فرکانس‌ها اگر نیمه‌ی اول آن را از 0 تا pi و نیمه‌ی دوم آن را از -pi تا 0 در نظر بگیریم، موقع ترسیم نمودار طیف به‌صورت متقارن نشان داده می‌شود، بدون اینکه جابه‌جایی در آرایه‌ی مقادیر fft انجام دهیم. به‌عبارت‌دیگر در این روش جابه‌جایی را در آرایه‌ی فرکانس انجام می‌دهیم (موقع تعریف مقادیر) و فرکانس‌های متناظر با مقادیر طیف را به‌نحوی در آرایه‌ی فرکانس قرار می‌دهیم تا موقع نمایش آن به‌صورت متقارن ترسیم شود. در این حالت چون آرایه‌ی مقادیر طیف را جابه‌جا نمی‌کنیم موقع محاسبه‌ی ifft نیازی به استفاده‌کردن از iffshift وجود ندارد؛ بنابراین بدون اینکه جابه‌جایی انجام دهیم می‌توانیم پردازش موردنظر را در حوزه‌ی فرکانس انجام دهیم.

برای اینکه آرایه فرکانس را به روش مطرح شده تعریف کنیم، از تابع fftfreq استفاده می‌کنیم. این تابع طول آرایه و فاصله‌ی بین نمونه‌ها (دوره تناوب نمونه‌برداری) را دریافت کرده و آرایه فرکانس را بر می‌گرداند.

مثال فیلتر میان‌گذر را این بار با استفاده از fftfreq پیاده‌سازی می‌کنیم. در این حالت موقع فیلترکردن (Y = X * bpf)  طیف‌ها به‌صورت نامتقارن هستند (از 0 تا 2*pi).

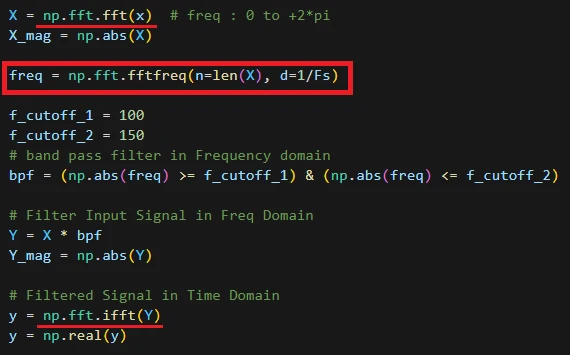
نمودار طیف فیلتر و سیگنال را ترسیم می‌کنیم. همان نتیجه‌ی قبلی را به دست می‌آوریم.

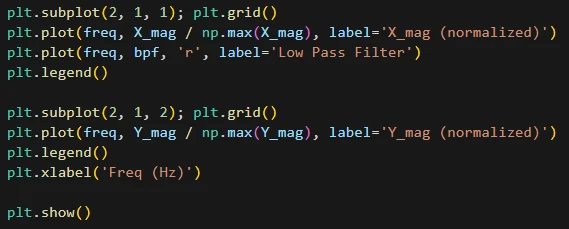
نمودار خروجی:

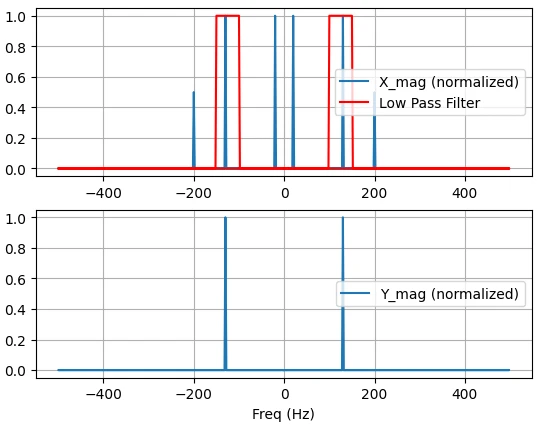
اگر نمودار دامنه طیف سیگنال و فیلتر را بدون ارسال آرایه فرکانس رسم کنیم، طیف به‌صورت نامتقارن (در بازه‌ی 0 تا 2*pi)  رسم می‌شود.

نمودار مقادیر آرایه‌ی فرکانس را رسم می‌کنیم. همان‌طور که انتظار داشتیم در نیمه‌ی اول آن مقادیر از صفر تا Fs/2 (در این مثال 500 هرتز)  قرار دارد و در نیمه‌ی دوم آن مقادیر از -Fs/2 تا صفر می‌باشد.

فایل کدهای این آموزش را می‌توانید از لینک گیت‌هاب زیر دانلود نمایید:

https://github.com/sphrk/array_indexing_examples_in_python