آموزش محاسبه سریع لگاریتم در FPGA – پیاده سازی
قسمت 2در قسمت قبلی آموزش با یک روش برای محاسبهی سریع تابع لگاریتم در سیستمهای دیجیتال آشنا شدیم. در این قسمت میخواهیم روش گفته شده را با زبان VHDL پیادهسازی کنیم.
در قسمت اول آموزش دیدیم که اگر بیایم و عدد رو بهصورت نماد علمی بنویسیم، لگاریتم آن برابر با Log(1.M)+E*Log(2) میشود و میتوانیم برای محاسبهی تقریبی مقدار لگاریتم عبارت E*Log(2) را محاسبه کنیم.
اعداد ممیز ثابت (Fixed Point)
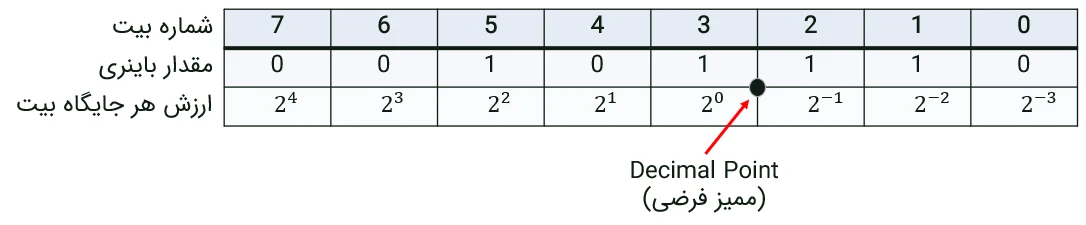
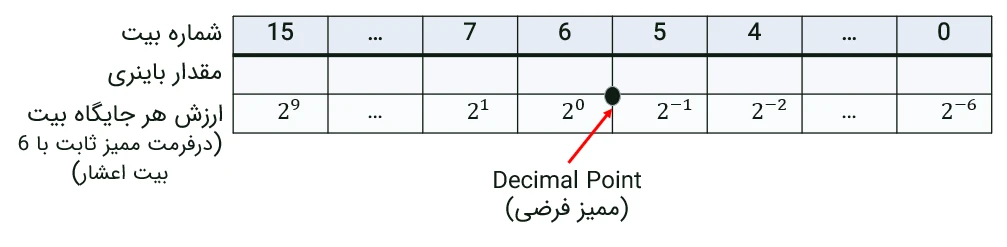
در پیادهسازی که میخواهیم انجام دهیم اعداد را در فرمت ممیز ثابت (Fixed Point) در نظر میگیریم. در فرمت Fixed Point دسیمال پوینت جابهجا میشود تا امکان نگهداری اعداد اعشاری فراهم شود. جابهجاکردن دسیمال پوینت یعنی درنظرگرفتن یک ممیز فرضی در رجیستر. در حالت عادی ارزش جایگاه بیتها بهصورت زیر میباشد (مقدار باینری عدد 46 نشاندادهشده است):
برای اینکه بتوان اعداد اعشاری را هم در رجیستر نگهداری کرد یه ممیز فرضی در نظر میگیریم یا بهعبارتدیگر دسیمال پوینت را جابهجا میکنیم و ارزش بیتهای بالاتر از ممیز فرضی توانهای مثبت 2 و ارزش بیتهای پایینتر از ممیز فرضی را توانهای منفی دو در نظر میگیریم. در مثال زیر ممیز فرضی را بین بیتهای 2 و 3 قرار دادهایم. بهعبارتدیگر از یک عدد 8 بیتی، 3 بیت را برای قسمت اعشاری در نظر گرفتهایم. عدد باینری که در مثال زیر نشاندادهشده است برابر است با مقدار 5.75 (5 ممیز 75 صدم).
توجه داشته باشید زمانی که برای نمایش اعداد از فرمت Fixed Point استفاده میکنیم، سیستم دیجیتال از محل ممیز اطلاع پیدا نمیکند. سیستم دیجیتال عددی که در فرمت Fixed Point هست را بهصورت یک عدد صحیح به آن نگاه میکند و محاسبات در فرمت Fixed Point را بهصورت محاسبات اعداد صحیح انجام میدهد.
ممیز فرضی که اشاره کردیم یک قرار داد در ذهن طراح میباشد و طبق آن محاسبات را انجام میدهد و موقع خواندن و نوشتن اعداد میداند که اعداد در چه فرمتی قرار دارند و چند بیت از آنها برای اعشار در نظر گرفته شده است.
مقدار باینری نشاندادهشده در حالت عادی برابر است با عدد 46 در مبنای 10. اگر بدانیم مقدار در فرمت Fixed Point بوده و 3 بیت برای اعشار در نظر گفته شده است، مقدار واقعی آن برابر با 5.75 میشود.
در مثال بالا با فرض اینکه 3 بیت برای اعشار در نظر گرفته شده است، ارزش بیت ها در حالت Fixed Point برابر است با ارزش بیت ها در حالت عادی تقسیم بر 2 به توان 3 . به مقدار 2 به توان 3 (2 به توان تعداد بیت های اعشار) مقیاس یا Scale گفته میشود. از مقدار مقیاس برای تبدیل عدد از فرمت اعشاری ممیز شناور به فرمت ممیز ثابت و برعکس استفاده می شود.
محاسبهی مقدار تقریبی لگاریتم
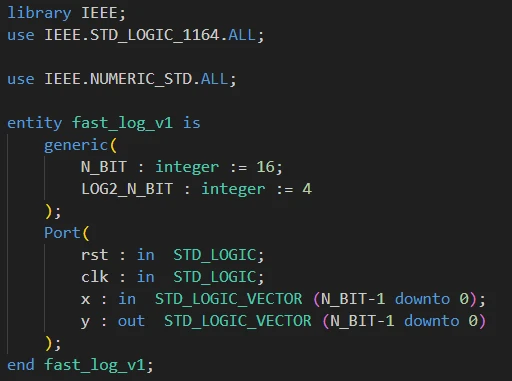
میخواهیم با استفاده از زبان توصیف سختافزار VHDL در FPGA یک مدار دیجیتال طراحی کنیم که مقدار تقریبی لگاریتم ورودی را محاسبه کند. در مداری که میخواهیم طراحی کنیم اعداد را 16 بیتی و در فرمت Fixed Point با 6 بیت اعشار در نظر میگیریم (از 16 بیت، 6 را برای اعشار در نظر میگیریم). ماژول ریست، کلاک و x را به عنوان ورودی دریافت کرده و در خروجی y مقدار لگاریتم x را محاسبه میکند. تعریف entity ماژول:
تعداد بیت رجیسترها و لگاریتم 2 تعداد بیت رجیستر ها را به صورت یک ژنریک تعریف می کنیم.
بهدستآوردن Exponent مقدار ورودی
سختافزاری که میخواهیم طراحی کنیم قرار است عبارت E*Log(2) را محاسبه کند. مقدار E همان Exponent عدد در حالت نمایش عدد بهصورت نماد علمی میباشد. در قسمت قبل دیدیم که مقدار Exponent همان مقدار توان ارزش جایگاه، پرارزشترین بیت 1 میباشد.
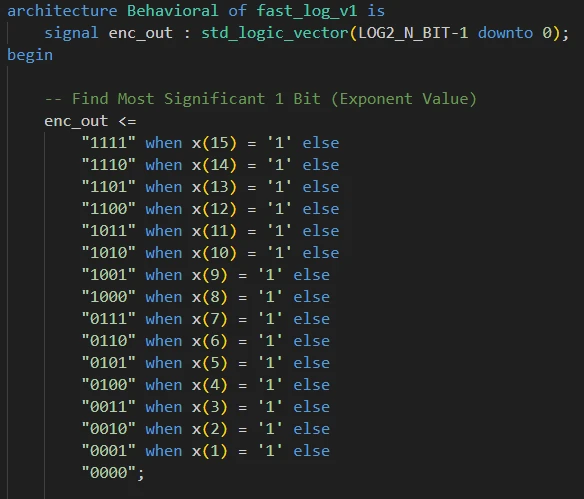
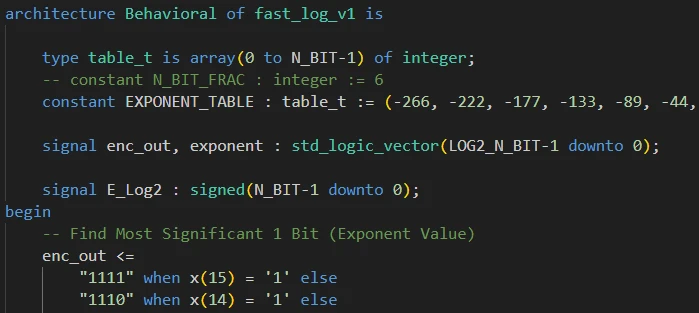
برای اینکه مقدار E*Log(2) را محاسبه کنیم نیاز هست که ابتدا مقدار E را به دست آوریم. برای این کار باید محل پرارزشترین بیت 1 از مقدار ورودی (x) را پیدا کنیم. برای پیاده سازی این قسمت از یک انکدر الویتدار (Priority Encoder) استفاده میکنیم. انکدر مقدار ورودی را دریافت کرده و در خروجی موقعیت بیت پرارزش ترین بیت 1 را تولید میکند. برای پیادهسازی انکدر الویتدار در VHDL از when else استفاده میکنیم. تعریف سیگنال خروجی انکدر و پیادهسازی انکدر الویتدار:
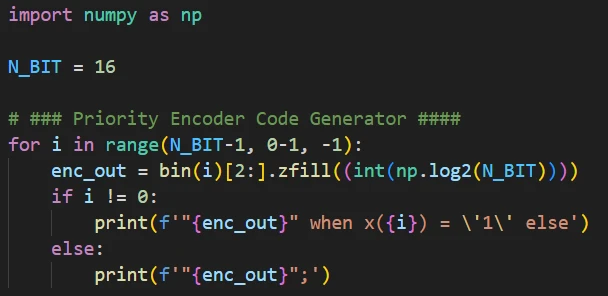
برای تولید کد مربوط به قسمت انکدر میتوانید از کد پایتون زیر استفاده کنید. این برنامه تعداد بیتها را دریافت کرده و متن کد VHDL مربوط به مدار موردنظر را تولید میکند و نیازی نیست که این کار تکراری را خودمان انجام دهیم. خروجی بهدستآمده را کپی کرده و در فایل مربوط به ماژول از آن استفاده میکنیم.
قسمت بهدستآوردن Exponent از روی ورودی را پیادهسازی کردیم. برای اینکه مقدار تقریبی لگاریتم ورودی را محاسبه کنیم کافیست مقدار Exponent را در Log(2) ضرب کرده و نتیجه را در خروجی قرار دهیم. برای اینکه هر بار نیازی به محاسبهی حاصلضرب نباشد و بدون استفاده از ضربکننده بتوان حاصل را به دست آورد، میتوان از یک Look Up Table استفاده کرد.
در این مثال تعداد بیت ورودی را 16 در نظر گرفتیم. پر ارزش ترین بیت 1 می تواند در هر یک از بیت های ورودی قرار بگیرد بنابراین 16 حالت مختلف داریم. هر یک از این 16 حالت Exponent را در Log(2) ضرب کرده و مقادیر بدست آمده را در یک جدول حافظه (LUT) ذخیره میکنیم تا بعدا از آن مقادیر استفاده کنیم.
✅نکته
محاسبهی مقادیر LUT با استفاده از پایتون
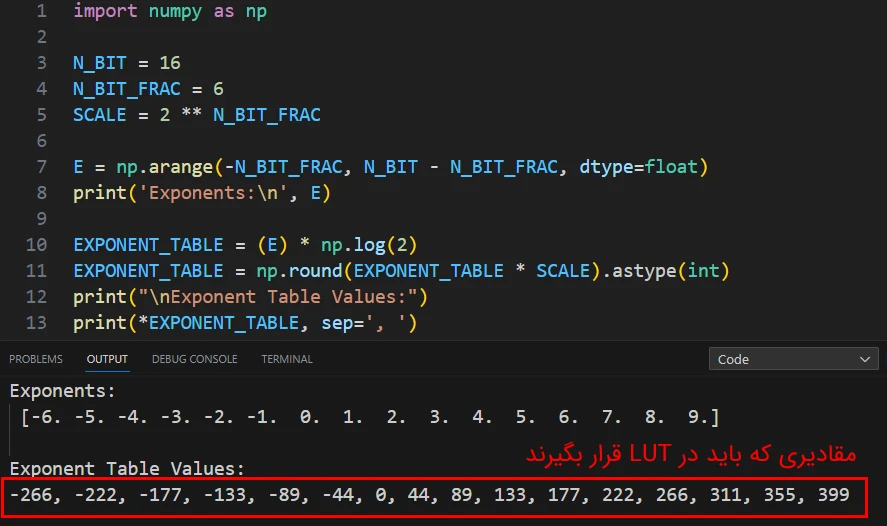
اعداد را در فرمت Fixed Point با 6 بیت اعشار در نظر گرفته ایم بنابراین Exponent ها از منفی 6 خواهد بود تا مثبت 9.
با استفاده از زبان برنامهنویسی پایتون مقادیری که در LUT باید قرار بگیرند را محاسبه میکنیم. مقادیر Exponent را در Log(2) ضرب کرده و نتیجه را به دست میآوریم. اعداد بهدستآمده در فرمت ممیز شناور (Floating Point) میباشند و باید آنها را به فرمت ممیز ثابتی که در نظر گرفتهایم تبدیل کنیم. اعداد Float بهدستآمده را به مقیاس (2 به توان 6) ضرب میکنیم. حاصل بهدستآمده ممکن است قسمت اعشاری داشته باشد برای همین مقادیر را round کرده (قسمت اعشاری مانده پس از مقیاسکردن را حذف میکنیم) و به integer تبدیل میکنیم با این کار اعداد اعشاری را به فرمت Fixed Point موردنظر تبدیل میکنیم. نتیجه بهدستآمده را در متغیر EXPONENT_TABLE ذخیره میکنیم. از
|
1 |
print(*EXPONENT_TABLE, sep=', ') |
برای چاپ مقادیر استفاده شده است. این خط بین مقادیر جدول کاما قرار داده و مقادیر را چاپ میکند. در خروجی این خط را کپی کرده و در فایل ماژول برای تعریف LUT از آن استفاده میکنیم.
برنامهٔ پایتون برای محاسبهٔ مقادیر جدول حافظه:
در فایل ماژول در داخل architecture و قبل از begin ابتدا یک type جدید به نام table_t تعریف میکنیم که یک آرایهٔ ۱۶تایی از اعداد integer میباشد. ثابت EXPONENT_TABLE را از این نوع تعریف کرده و در آن مقادیر جدول که قبلاً به دست آوردیم را قرار میدهیم.
یک سیگنال به نام exponent هم طول با خروجی انکدر تعریف میکنیم و در هر لبهی بالارونده کلاک، خروجی انکدر را در exponent رجیستر میکنیم؛ بنابراین در هر کلاک در رجیستر exponent، موقعیت پرارزشترین بیت ورودی قرار میگیرد.
در کلاک بعدی، از مقدار موجود در رجیستر exponent استفاده کرده و این آدرس از LUT را انتخاب میکنیم یا بهعبارتدیگر اندیس exponent از LUT را انتخاب میکنیم. اندیس آرایه در VHDL باید از نوع integer باشد. خروجی انکدر که در exponent قرار میگیرد از نوع std_logic_vector میباشد. برای اینکه از exponent که از نوع std_logic_vector هست بهعنوان اندیس استفاده کنیم ابتدا آن را به unsigned و سپس به integer بهصورت زیر تبدیل میکنیم:
|
1 |
to_integer(unsigned(exponent)) |
سپس این اندیس از LUT را بهصورت زیر انتخاب میکنیم:
|
1 |
EXPONENT_TABLE(to_integer(unsigned(exponent))) |
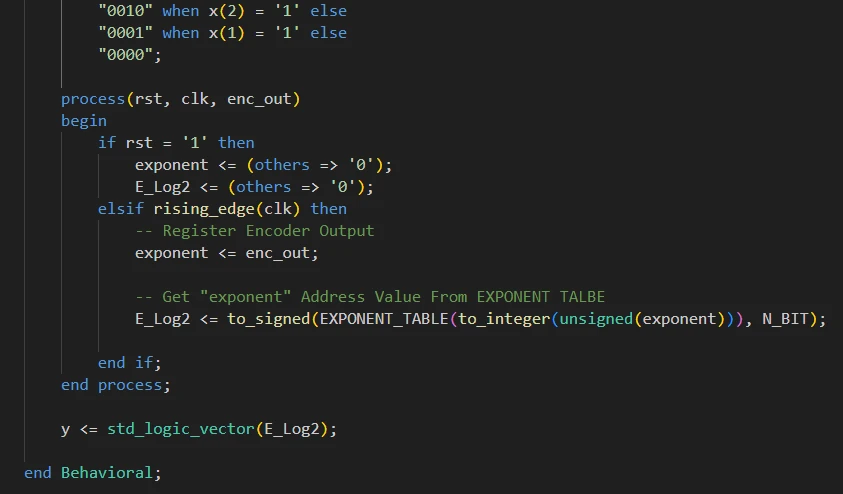
مقادیری که در هر آدرس از جدول قرار گرفتهاند، مقدار E*Log(2) در فرمت Fixed Point میباشد. با انتخاب این اندیس از جدول، مقدار تقریبی لگاریتم ورودی را به دست میآوریم. مقادیر موجود در آرایه از نوع integer میباشند. خروجی آرایه را با استفاده از تابع to_signed به عدد علامتدار 16 بیتی تبدیل میکنیم و نتیجه را در رجیستر 16 بیتی E_Log2 ذخیره میکنیم.
E_Log2 <= to_signed(EXPONENT_TABLE(to_integer(unsigned(exponent))), N_BIT);
رجیستر کردن خروجی LUT در رجیستر E_Log2 را در هر لبه بالاروندهی کلاک انجام میدهیم.
مقدار تقریبی لگاریتم ورودی در رجیستر E_Log2 قرار میگیرد. در بیرون از process مقدار رجیستر E_Log2 را به std_logic_vector تبدیل کرده و به خروجی y ماژول وصل میکنیم. پیادهسازی ماژول را تکمیل کردیم. ماژول در هر لبه بالارونده کلاک مقدار Exponent ورودی را پیدا کرده و رجیستر میکند. در کلاک بعدی از روی آن مقدار تقریبی لگاریتم را به دست آورده و در خروجی رجیستر میکند. با تأخیر 2 کلاک توانستیم مقدار تقریبی لگاریتم ورودی را محاسبه کنیم.
بهتر است ورودی را در هر لبهی بالارونده کلاک در یک رجیستر داخلی ذخیره کرده و سپس از روی مقدار ورودی رجیستر شده مقدار Exponent را به دست آوریم و آن را رجیستر کرده و در کلاک بعدی آن اندیس از LUT را در رجیستر خروجی قرار دهیم.
برای ماژولی که پیادهسازی کردیم یک تست بنچ (Test Bench) نوشته و عمل کرد آن را بررسی میکنیم.
تست بنچ
اعداد را 16 بیتی و در فرمت ممیز ثابت با 6 بیت اعشار در نظر گرفته ایم (مقادیر جدول با این فرمت محاسبه شدهاند). مقداری که در ورودی ماژول قرار میگیرد باید در این فرمت ممیز ثابت باشد، همچنین مقدار خروجی ماژول هم در این فرمت ممیز ثابت تولید میشود. برای اینکه در تست بنچ به راحتی بتوانیم مقادیر اعشاری مورد نظر را در ورودی قرار دهیم و مقادیر خروجی ماژول را به راحتی مشاهده کنیم از دو سیگنال کمکی از نوع real استفاده میکنیم. برای اینکه در فایل تست بنچ از اعداد real استفاده کنیم کتابخانه math_real را به فایل تست بنچ اضافه میکنیم:
|
1 |
use ieee.math_real.all; |
قبل از begin قسمت architecture، تعداد بیت رجیسترها و تعداد بیتی که برای اعشار در نظر گرفته شده است (6 بیت) را به صورت ثابت تعریف میکنیم.
|
1 2 3 |
constant N_BIT : integer := 16; constant N_BIT_FRAC : integer := 6; |
ثابت SCALE (مقیاس) را از نوع real تعریف کرده و در آن مقدار مقیاس فرمت ممیز ثابتی که در نظر گرفتهایم را قرار میدهیم. از روی ثابتهایی که تعریف کردیم مقدار مقیاس را محاسبه میکنیم.
|
1 |
constant SCALE : real := 2.0 ** real(N_BIT_FRAC); |
دو سیگنال کمکی x_r و y_r را از نوع real تعریف میکنیم.
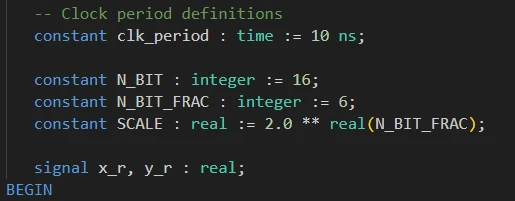
برای اینکه هنگام مقداردهی ورودی و خواندن خروجی ماژول در تست بنچ را بهراحتی بتوانیم انجام دهیم، مقدار اعشاری ورودی موردنظر (در مبنای 10) را در سیگنال کمکی x_r قرار میدهیم. میدانیم مقدار ورودی ماژول باید در فرمت ممیز ثابت باشد بنابراین بایستی مقدار اعشاری x_r را به فرمت ممیز ثابت موردنظر تبدیل کنیم.
برای تبدیل x_r به ممیز ثابت، ابتدا آن را به ثابت مقیاس که تعریف کردهایم ضرب میکنیم. حاصل بهدستآمده ممکن است قسمت اعشاری داشته باشد، به همین دلیل حاصل را round میکنیم تا یک عدد کاملاً صحیح به دست آوریم. تابع round در کتابخانهی math_real تعریف شده است و مقدار ورودی آن باید از نوع real باشد. خروجی تابع round از نوع real میباشد، آن را به integer تبدیل میکنیم. با این کار معادل ممیز ثابت مقدار اعشاری x_r را به دست میآوریم. ورودی ماژول از نوع std_logic_vector میباشد، ازاینرو مقدار integer بهدستآمده را ابتدا با استفاده از تابع to_unsigned به یک عدد بدون علامتدار N_BIT (16 بیتی) تبدیل کرده و سپس آن را به std_logic_vector تبدیل میکنیم و به ورودی x وصل میکنیم.
|
1 |
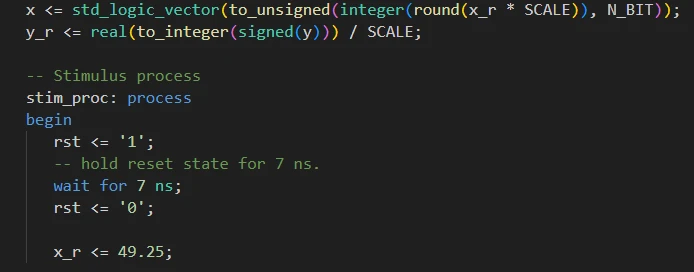
x <= std_logic_vector(to_unsigned(integer(round(x_r * SCALE)), N_BIT)); |
این خط را در خارج از process شبیهسازی مینویسیم. زمانی که بخواهیم در ورودی ماژول مقداری قرار دهیم، کافیست مقدار اعشاری موردنظر را در سیگنال x_r قرار دهیم، تبدیلات لازم برای تبدیلکردن آن به یک عدد ممیز ثابت 16 بیتی با 6 بیت اعشار توسط خط بالا انجام میشود.
همانطور که قبلاً هم اشاره کردیم، خروجی هم در فرمت ممیز ثابت میباشد، میتوانیم خروجی ماژول را از فرمت ممیز ثابت به فرمت اعشاری در مبنای 10 تبدیل کنیم تا خواندن مقدار بهدستآمده راحتتر باشد. برای این کار خروجی ماژول (y) که از نوع std_logic_vector میباشد را به signed تبدیل کرده و سپس با استفاده از to_integer به نوع integer تبدیل میکنیم. مقدار بهدستآمده را به نوع real تبدیل کرده و آن را به مقیاس تقسیم میکنیم تا مقدار واقعی خروجی را به دست آوریم.
|
1 |
y_r <= real(to_integer(signed(y))) / SCALE; |
این خط را نیز در خارج از process شبیهسازی مینویسیم.
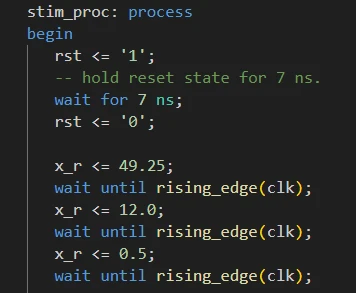
در داخل process شبیهسازی ابتدا مدار را ریست کرده (rst=1) و پس از تأخیر کوتاهی از حالت ریست در میآوریم (rst=0). پس از ریستکردن مدار مقدار ورودی موردنظر 49.25 را در سیگنال کمکی x_r قرار میدهیم و شبیهسازی را اجرا میکنیم.
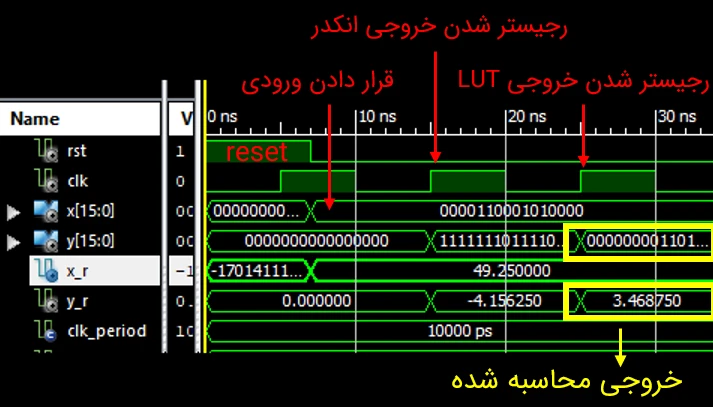
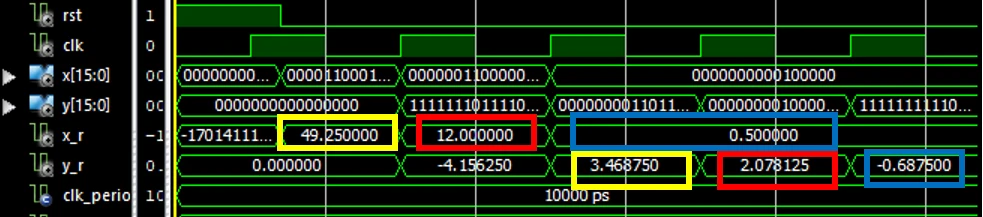
خروجی شبیهسازی
پیادهسازی که انجام دادهایم بهصورت پایپ لاین میباشد و این امکان را فراهم میکند که در هر کلاک به ماژول ورودی ارسال کنیم. در تست بنچ پس از اینکه مقدار اول را در ورودی قرار دادیم یک کلاک صبر کرده و مقدار جدید را در ورودی قرار میدهیم.
خروجی شبیهسازی:
مباحثی که در آموزش یاد گرفتیم به شرح زیر میباشد:
- آشنایی با اعداد ممیز ثابت
- محاسبهی مقادیر LUT
- پیادهسازی سختافزار برای محاسبه سریع لگاریتم
- آشنایی با نوع real در VHDL
- تبدیل اعداد ممیز ثابت به ممیز شناور و برعکس در تست بنچ
همانطور که در قسمت قبلی آموزش هم اشاره کردیم با استفاده از LUT برای قسمت Exponent میتوان بهصورت تقریبی مقدار لگاریتم را محاسبه کنیم. در این آموزش این روش را پیادهسازی کردیم. برای اینکه مقدار لگاریتم را با دقت بالاتری محاسبه کنیم نیاز هست که از قسمت اعشاری عدد هم استفاده کنیم. در قسمت بعدی آموزش، قسمت مربوط به جدول Mantissa را پیادهسازی میکنیم.
فایلهای این آموزش را میتوانید از لینک گیتهاب زیر دانلود نمایید:
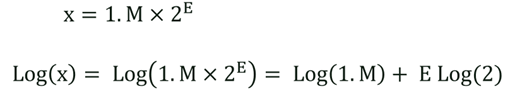






















سیسوگ با افتخار فضایی برای اشتراک گذاری دانش شماست. برای ما مقاله بنویسید.