آشنایی با همینگ کد و لذت یک ارتباط امن و بدون خطا
ارتباط! بله مقولهی مهم عصر جدید، ارتباط است. ارتباط انسان و ماشین، ارتباط با آدم فضاییها، ارتباط ماشین با ماشین و یا حتی ارتباط انسان با انسان. در برقراری ارتباط همیشه چالشی نهفته است و آنهم تفهیمِ مفهوم است؛ این که سعی کنید به نحوی مطلب را بیان کنید که مخاطب منظور شما را متوجه شود. شاید در نگاه اول چنان مقوله مهمی به نظر نرسد ولی فرض کنید انسانها توانسته باشند تمدنی در منظومه شمسی را شناسایی کنند و سعی کنند برای آنها پیامی از صلح و دوستی ارسال کنند. حال اگر تمدن مذکور آن پیام را تهدید یا دعوت به جنگ استنباط کند، چه اتفاقی روی خواهد داد؟!
یا فرض کنید دو دستگاه در خط تولید یک کارخانه، اطلاعاتی را با هم تبادل میکنند. اگر عوامل محیطی باعث شوند که اطلاعات بهصورت صحیح بین دستگاهها ردوبدل نشود، قاعدتاً عملکرد دستگاهها مختل خواهد شد! مسئلهی چالشبرانگیز هر ارتباطی، صحت آن است؛ این که به نحوی گیرندهی پیام مطمئن باشد منظور شما از پیام چیست و هیچگونه شکی در آن وجود نداشته باشد. اما چطور میتوان به این مهم دست پیدا کرد؟ چطور میشود پیامها را به نحوی انتقال داد که گیرنده از صحت آنها اطمینان حاصل کند؟ برای روشن شدن مسئله با سیسوگ همراه شوید. ما در این مقاله به بررسی یکی از راههای خطایابی ارتباطها میپردازیم.
معرفی کانالهای ارتباطی
اگرچه زیاد فرقی نمیکند که کانال ارتباطی چه باشد، صوت یا نوشتار، آنالوگ یا دیجیتال، سریال یا پارالل، دیفرانسیلی یا غیر دیفرانسیلی اما همه و همه در برابر عوامل بیرونی (نویز) تأثیر پذیر هستند و ممکن است صحت آنها دچار تغییر شود. البته منکر این مهم نیستیم که بنا به ماهیت، تأثیر پذیری برخی از آنها از عوامل خارجی، کم است ولی تغییر ناخواسته اجتنابناپذیر است و نمیتوان مطمئن بود که اطلاعات در مسیر دستخوش تغییر نشدهاند.
ممکن است برای انتقال از پروتکل سریال یا مودمهای آنالوگ یا حتی ارتباط رادیویی استفاده کرده باشید. در این مقاله، بستر انتقال اطلاعات چندان دارای اهمیت نیست، مسئلهی مهم این است که اطلاعات دریافتی (از هر بستری) صحیح است یا اشتباه؟
بررسی اجمالی راههای خطایابی
در یک ارتباط دیجیتال، راههای زیادی برای تشخیص خطا وجود دارد. رایجترین روش تشخیص در ارتباط سریال یا حتی پارالل، قرار دادن بیت توازن (Parity bit) است. طبق تعریف بیت توازن میتواند زوج یا فرد باشد.
هنگامیکه از توازن زوج استفاده میشود، اگر تعداد یکهای ورودی زوج باشد، بیت توازن صفر میشود و بالعکس
هنگامیکه از توازن فرد استفاده میشود، اگر تعداد یکهای ورودی فرد باشد، بیت توازن صفر میشود و بالعکس.
اما این روش خود دارای خطا است و ممکن است شرایطی ایجاد شود که خطا تشخیص داده نشود. مثلاً فرض کنید نویز باعث تغییر جای بیتها شده باشد. گیرنده با توجه به وضعیت Parity متوجه نخواهد شد که جایگاه دو بیت تعویض شده است، چراکه تناسب بیتهای 1 به هم نخورده است. یا این که نویز باعث تغییر وضعیت دو بیت در دادههای ارسالی شده باشد.
همانطور که میبینید Parity bit روش خوبی است اما باز احتمال خطا هرچند کم، ولی وجود دارد.
یکی دیگر از روشهای مورداستفاده در خطایابی، قرار دادن یک بایت انتهای بایتهای ارسالی است. فرض کنید قرار است 10 بایت داده را منتقل کنیم، یک بایت 11 ام هم در نظر میگیریم که حاصل جمع 10 بایت اول را در خود جای داده است. این روش را checksum گویند. این روش نیز دارای خطا است. اگر موقعیت بایتها عوض شود، همچنان توسط گیرنده قابلتشخیص نیست. برای بهتر شدن میتوان بهجای حاصل جمع، از الگوریتم CRC نیز استفاده کرد که به محل قرارگیری بایتها نیز حساس است ولی همچنان خالی از احتمال خطا نخواهد بود.
البته صدها روش مشابه دیگر هم وجود دارند. همهی این روشها برای تشخیص خطا هستند و به ما میگویند دادههای ارسالی به دلایلی دارای صحت نیستند و در مسیر، دستخوش تغییر شدهاند.
اما آیا روشی وجود دارد که با استفاده از آن بتوانیم دادههای دریافتی که دارای خطا هستند را ترمیم کنیم و دیتای صحیح را از آن استخراج کنیم؟
همینگ کد چیست؟
همانطور که اشاره شد، روشهای زیادی برای پیدا کردن خطای دادههای ارسالی وجود دارد. اما چطور میشود بعد از شناسایی خطای مربوطه، آن را ترمیم کرد؟ در این حوزه نیز الگوریتمها و پروتکلهای مختلفی وجود دارد. یکی از این روشها، روش همینگ است. ریچارد همینگ ریاضیدان آمریکایی (سومین برندهی جایزه تورینگ)، مقالهی مشهور خود را در سال 1950 هنگامیکه در شرکت IBM مشغول به کار بود منتشر کرد. این مقاله دربارهی آشکارسازی و تصحیح خطا بود و مفاهیم کد همینگ، فاصلهی همینگ و پنجرهی همینگ را تعریف کرد.
در کد همینگ گیرنده علاوه بر تشخیص صحیح خطا (برخلاف بیت توازن و checksum، قادر به اصلاح خطا نیز است. البته توجه داشته باشید که هر الگوریتمی محدودیتهای خاص خود را دارد. کد همینگ فقط قادر به تصحیح یک بیت است ولی بهدرستی خطاهای اتفاق افتاده را تشخیص میدهد.
همینگ کد چطور کار میکند؟
برای روشن شدن هرچه بیشتر قضیه و نگاه کاربردی به آن، سعی میکنیم که همینگ کد را در قالب یک مثال ساده آموزش دهیم. فرض کنید که قصد داریم دادهای را از یک فرستنده به گیرندهای ارسال کنیم. داده ما 8 بیت طول دارد. برای تصحیح خطا در دادههای 8 بیتی بنا به نظریهی فاصلهی همینگ، نیاز به 4 بیت دادهی تصحیح خطا خواهیم داشت. پس در مجموع برای ارسال 8 بیت داده با استفاده از همینگ کد، نیاز به 12 بیت خواهیم داشت.
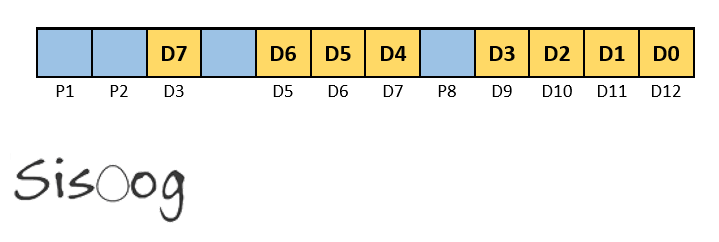
همانطور که در تصویر فوق مشاهده میکنید، محل قرارگیری بیتهای داده در ساختار همینگ کد پشت سرهم نیست؛ مثلاً آخرین بیت از دادهی ارسالی (D7) باید در موقعیت سوم قرار بگیرد. خانههای مشخصشده با رنگ زرد، محل قرارگیری دادهها هستند و خانهی مشخصشده با رنگ آبی محل قرارگیری بیتهای توازن هستند. قبلاً اشاره شد که برای ارسالهای 8 بیتی، نیاز به 4 بیت توازن داریم که با نامهای P1,P2,P4,P8 مشخص شدهاند.
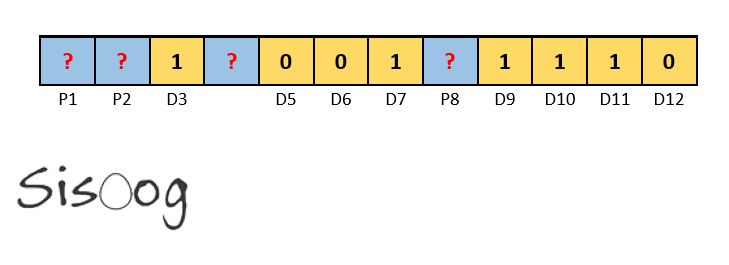
فرض کنید قصد داریم دادهی 0x9E را ارسال کنیم. معادل باینری آن 10011110 میشود. با جای گذاری آن، تصویری مطابق شکل زیر خواهیم داشت:
حال باید بیتهای توازن را محاسبه و جای گذاری کنیم. هر بیت توازن در واقع توازن زوج از بیتهای 1 است.
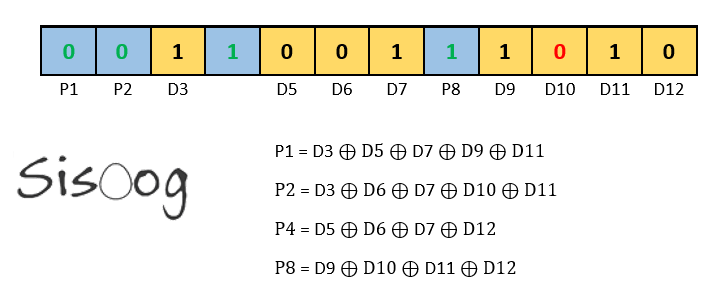
بهعنوان نمونه بیت توازن P1، توازن زوج از بیتهای 3 و 5 و 7 و 9 و 11 است. تعداد مقدار 1 در این چهار بیت، عدد زوج 4 است (تنها بیت 5 صفر است)؛ بنابراین P1 باید صفر باشد. مابقی بیتها را نیز مطابق فرمول ارائهشده در عکس محاسبه میکنیم که مقدار P2 یک، مقدار P4 یک و مقدار P8 نیز صفر میشود.
با جای گذاری دادههای موردنیاز، داده ارسال میشود و در گیرنده دریافت میشود؛ اما به دلیل نویزهای محیطی، داده با خطا و تغییر بیت D10 از 1 به صفر دریافت شده است.
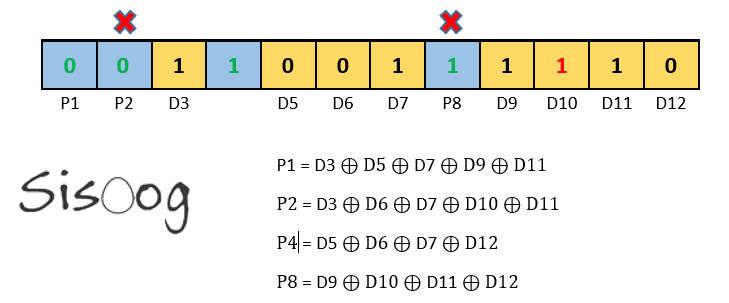
گیرنده شروع به محاسبهی بیتهای توازن میکند. با توجه به تغییر وضعیت D10 و با توجه به تأثیر D10 بر روی P2 و P8، این دو بیت توازن دارای مقداری صحیح نخواهند بود درحالیکه دو بیت توازن P1 و P4 دارای مقداری صحیح هستند.
برای پیدا کردن بیتی که دچار خطا شده، کافی است که ارزش بیتی P2 و P8 را با هم جمع کنیم؛ یعنی 2+8 که میشود بیت دهم.
همانطور که مشاهده کردید بهراحتی علاوه بر تشخیص خطا، قادر خواهیم بود خطای ایجادشده را تصحیح نیز کنیم. همینگ کد کاربردهای فراوانی از جمله در ارتباطهای رادیویی و شبکهای دارد. این الگوریتم باعث کاهش خطا و رفع آن میشود.
برای درک بهتر میتوانید به ویدئوی زیر توجه کنید:




















سیسوگ با افتخار فضایی برای اشتراک گذاری دانش شماست. برای ما مقاله بنویسید.