پیاده‌سازی فیلتر میانه و تولید نویز گوسی ترکیبی در پایتون

در قسمت قبل با فیلترکردن سیگنال در حوزه‌ی فرکانس آشنا شدیم. در این قسمت می‌خواهیم با استفاده از array indexing ، فیلتر میانه را پیاده‌سازی کنیم و نحوه‌ی تولید نویز ضربه‌ای گوسی ترکیبی را یاد بگیریم. از فیلتر میانه می‌توان برای حذف نویز ضربه‌ای از سیگنال و یا حذف داده‌های پرت (outlier) استفاده کرد. برای مثال در پردازش تصویر برای حذف نویز فلفل‌نمکی از فیلتر میانه استفاده می‌شود. نویز فلفل‌نمکی یک نویز ضربه‌ای می‎باشد و در تصویر باعث می‌شود مقدار یک پیکسل به بیشترین یا کمترین سطح خاکستری (سفید یا سیاه) تبدیل شود. با اعمال فیلتر میانه دو بعدی به تصویر، می‌توان نویز فلفل‌نمکی را حذف کرد.

در فیلتر میانه ابتدا مقادیر با دامنه‌های بزرگ یا به‌عبارت‌دیگر مقادیر ضربه‌ای را پیدا می‌کنیم و سپس در آن نقطه یک کرنل در نظر می‌گیریم. میانه‌ی مقادیر موجود در کرنل را به دست آورده و جایگزین مقدار ضربه‌ای می‌کنیم. جایگزین‌کردن مقدار میانه‌ی مقادیر موجود در حوالی مقدار ضربه‌ای باعث می‌شود دامنه‌های بزرگ که به احتمال زیاد مقادیر آغشته به نویز ضربه‌ای هستند حذف شده و سیگنال هموار (smooth) شود. در این آموزش فیلتر میانه یک بعدی را در پایتون پیاده‌سازی کنیم.

کدهای پایتون نوشته در این آموزش، در یک فایل ژوپیتر نوت‌بوک نوشته شده‌اند. لینک دانلود فایل ژوپیتر نوت‌بوک مربوط به این آموزش در انتهای صفحه قرار داده شده است.

برای تعریف آرایه‌ها کتابخانه numpy و برای ترسیم نمودار کتابخانه matplotlib را import می‌کنیم.

یک سیگنال سینوسی تعریف می‌کنیم. می‌خواهیم به 9 مقدار از سیگنال نویز ضربه ای اضافه کنیم. با تابع randint به تعداد 9 تا اندیس تصادفی تولید کرده (9 مقدار تصادفی صحیح که در بازه‌ی صفر تا طول آرایه‌ی سیگنال قرار دارد تولید می‌کنیم) و به مقدار این اندیس‌ها در آرایه نویز اضافه می‌کنیم. به این تعداد نویز گوسی با میانگین صفر و انحراف معیار 5 تولید کرده و به اندیس های انتخاب شده از آرایه سیگنال اضافه می‌کنیم.

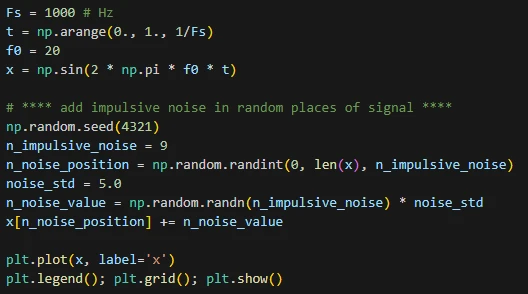
نمودار خروجی:

فیلتر میانه

اولین قدم در فیلتر میانه تشخیص مقادیر با دامنه‌ی بزرگ می‌باشد. به‌عبارت‌دیگر ابتدا باید مقادیری که احتمالاً آغشته به نویز ضربه‌ای هستند را پیدا کنیم. برای این کار ابتدا یک آستانه در نظر گرفته و مقادیری که بزرگ‌تر از آستانه هستند را به‌عنوان مقادیر با دامنه‌ی بزرگ در نظر می‌گیریم. برای انتخاب مقدار آستانه باید بازه‌ی تغییرات سیگنال در حالت بدون نویز را بدانیم و از روی آن یک آستانه مناسب در نظر بگیریم تا مقادیری از سیگنال که از آستانه بزرگ‌تر هستند را به‌عنوان مقادیر ضربه‌ای در نظر بگیریم.

در این مثال سیگنال را سینوسی در نظر گرفته‌ایم. مقدار آستانه را 2 فرض می کنیم. سیگنال را آستانه گذاری کرده و نمودار ماسک بدست آمده و سیگنال را رسم می‌کنیم.

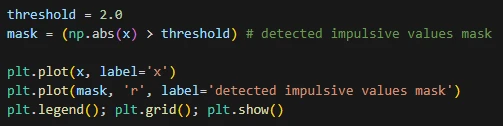
نمودار خروجی:

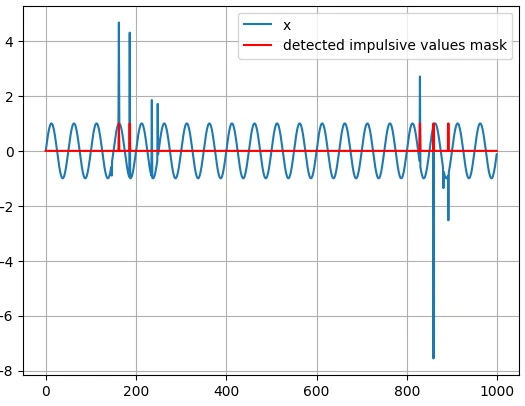
می‌توان مشاهده کرد در جاهایی که قدرمطلق مقدار سیگنال از آستانه بزرگ‌تر می‌باشد، مقدار ماسک True و در بقیه جاها مقدار آن False می‌باشد.

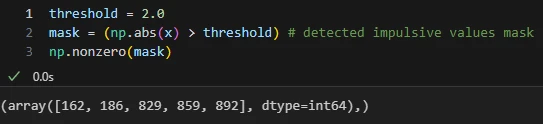
حال از روی ماسک به‌دست‌آمده می‌خواهیم اندیس مقادیر ضربه‌ای را پیدا کنیم. به‌عبارت‌دیگر می‌خواهیم اندیس‌هایی از آرایه‌ی ماسک که مقدار آن True هست را پیدا کنیم. برای این کار از تابع nonzero استفاده می‌کنیم. این تابع اندیس مقادیری از آرایه که غیرصفر هستند را در هر بعد از آرایه بر می‌گرداند.

در مثال زیر عملکرد این تابع را می‌توان مشاهده کرد.

با استفاده از nonzero محل مقادیر ضربه‌ای را از روی آرایه‌ی ماسک به دست می‌آوریم.

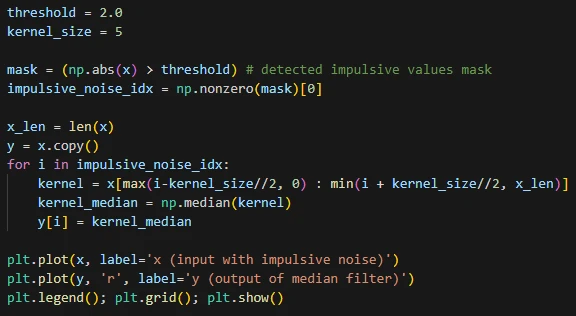
حال می‌خواهیم در هر یک از محل‌هایی که مقدار ضربه‌ای وجود دارد یک کرنل در نظر بگیریم و میانه‌ی مقادیر موجود در کرنل را به دست آوریم. اندازه‌ی کرنل را 5 در نظر می‌گیریم. هرچقدر سیگنال به نویز ضربه‌ای شدیدتری آغشته باشد (تعداد مقادیر با دامنه‌ی بزرگ زیاد باشد) احتمال اینکه چند مقدار ضربه‌ای در داخل یک کرنل قرار بگیرند (در کنار هم باشند) بیشتر می‌شود برای همین در این شرایط باید سایز کرنل را بزرگ‌تر در نظر بگیریم (برای مثال 9 یا 11) تا موقع محاسبه‌ی میانه، مقادیر با دامنه‌ی بزرگ به‌عنوان میانه انتخاب نشوند.

برای فیلترکردن، یک حلقه‌ی for می‌نویسیم و در هر تکرار آن اندیس‌هایی که مقدار ضربه‌ای در آن‌ها قرار دارد را به دست آورده و در آن محل یک کرنل در نظر می‌گیریم. میانه‌ی مقادیر انتخاب شده را به دست می‌آوریم. مقدار میانه را جایگزین مقدار ضربه‌ای می‌کنیم.

نمودار خروجی:

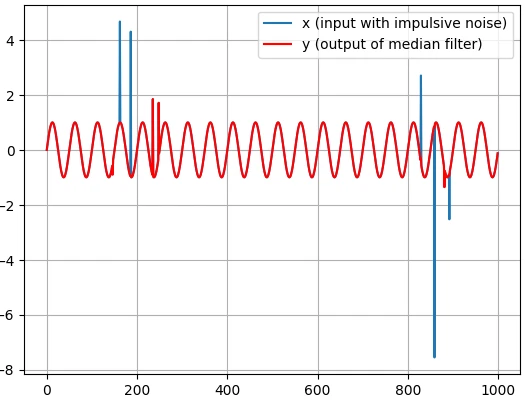
می‌توان مشاهده کرد در سیگنال خروجی، مقادیر با دامنه‌های بزرگ حذف شده‌اند و سیگنال هموارتری به‌دست‌آمده است.

یک تابع برای فیلتر میانه یک بعدی می‌نویسیم.

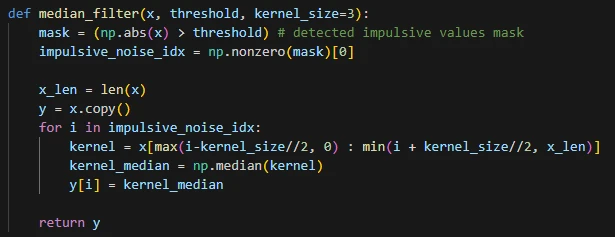
سیگنال نویزی x را این بار با آستانه 1 و سایز کرنل 5 فیلتر می‌کنیم.

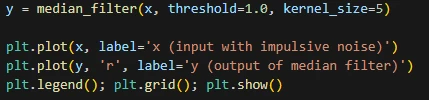
نمودار خروجی:

نویز گوسی ترکیبی (Gaussian Mixture)

برای تولید نویز ضربه‌ای می‌توان از مدل گوسی ترکیبی استفاده کرد. در گوسی ترکیبی، دو توزیع گوسی در نظر می‌گیریم (در حالت کلی می‌تواند بیشتر هم باشد). ابتدا به‌صورت تصادفی با توزیع برنولی انتخاب می‌کنیم که از کدام توزیع گوسی برای تولید نمونه‌ی تصادفی استفاده کنیم. پس از انتخاب‌کردن توزیع، مقدار تصادفی را با آن توزیع تولید می‌کنیم. برای هر نمونه این کار را تکرار می‌کنیم.

بزرگ درنظرگرفتن واریانس یکی از گوسی‌ها باعث می‌شود احتمال رخ‌دادن مقادیر با دامنه‌ی بزرگ در این توزیع بیشتر از دیگری باشد. این موضوع باعث می‌شود در خروجی برخی مقادیر دامنه‌ی بزرگ‌تری داشته باشند.

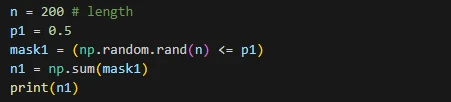
می‌خواهیم یک سیگنال نویز به‌صورت گوسی ترکیبی به طول n ایجاد کنیم. همان‌طور که اشاره کردیم اولین قدم انتخاب توزیع گوسی با توزیع برنولی است. با توزیع برنولی انتخاب می‌کنیم که در هر نمونه از کدام توزیع گوسی برای تولید مقدار تصادفی استفاده کنیم. تابع rand اعداد تصادفی با توزیع یکنواخت در بازه‌ی صفر تا 1 تولید می‌کند. با این تابع یک آرایه‌ی تصادفی به طول n ایجاد کرده و با p1 آستانه‌گذاری می‌کنیم. مقدار p1 احتمال انتخاب‌شدن توزیع گوسی اول می‌باشد؛ بنابراین توزیع گوسی دوم با احتمال 1 – p1 انتخاب می‌شود. در این مثال احتمال انتخاب‌شدن توزیع گوسی اول (p1) را 0.5 در نظر گرفته‌ایم.

با آستانه‌گذاری آرایه‌ی تصادفی تولید شده با rand و انتخاب مقادیر کمتر از p1 در آن، محل نمونه‌هایی که باید از توزیع گوسی اول برای تولید نمونه‌ی تصادفی استفاده کنیم را به دست می‌آوریم. نتیجه‌ی آستانه‌گذاری را در mask1 ذخیره می‌کنیم. همه مقادیر این آرایه‌ را با هم جمع کرده و در n1 ذخیره می‌کنیم. می‌دانیم معادل integer مقدار True، یک صحیح و معادل False هم صفر می‌باشد. جمع‌کردن همه‌ی مقادیر آرایه‌ی mask1 باعث می‌شود تعداد Trueها را به دست آوریم که این مقدار برابر هست با تعداد نمونه‌های تصادفی که باید با توزیع گوسی اول آن‌ها را تولید کنیم.

واریانس توزیع گوسی اول را 5 و واریانس توزیع دوم را 100 در نظر می‌گیریم. میانگین هر دو توزیع را صفر فرض می‌کنیم. با استفاده از تابع randn اعداد تصادفی با توزیع نرمال (گوسی با میانگین صفر و ورایانس 1) تولید می‌کنیم. رادیکال واریانس (انحراف معیار)  را به اعداد تصادفی تولید شده ضرب می‌کنیم تا واریانس آن را به مقدار مورد نظر تغییر دهیم.

یک آرایه‌ی تمام صفر به طول n ایجاد می‌کنیم و در متغیر noise قرار می‌دهیم. به تعداد n1 نمونه عدد تصادفی از توزیع گوسی اول تولید می‌کنیم (np.random.randn(n1) * np.sqrt(var1)) و این مقادیر را در noise[mask1] قرار می‌دهیم (اندیس‌هایی از آرایه‌ی noise که مقدار mask1 در آن‌ها True است).

در ادامه به تعداد n – n1  نمونه تصادفی با توزیع گوسی با واریانس var2 ایجاد کرده و در noise[~ mask1] قرار می‌دهیم. با not کردن mask1، موقعیت‌هایی که باید نمونه‌های تصادفی از توزیع گوسی دوم قرار بگیرند را به دست می‌آوریم. این اندیس‌ها را انتخاب کرده و مقادیر تصادفی را در آن‌ها قرار می‌دهیم. نمودار noise را رسم می‌کنیم.

نمودار خروجی:

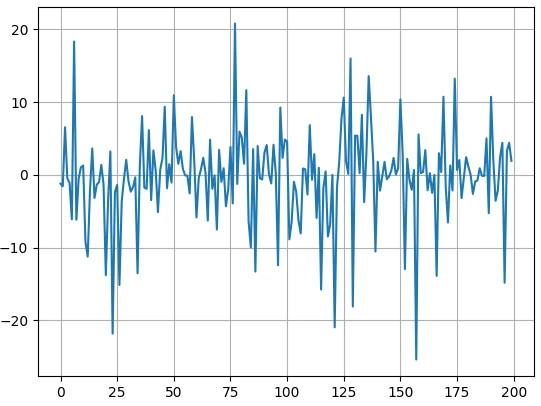
واریانس گوسی دوم را بزرگ‌تر از توزیع اول در نظر گرفته بودیم. این موضوع باعث شده است نمونه‌هایی با مقدار بزرگ ایجاد شود.

برای تولید نویز گوسی ترکیبی یک تابع می‌نویسیم. تابع طول آرایه، واریانس توزیع گوسی اول، واریانس توزیع گوسی دوم و احتمال انتخاب‌شدن گوسی اول را در ورودی دریافت کرده و در خروجی آرایه‌ی نویز را با طول موردنظر برمی‌گرداند.

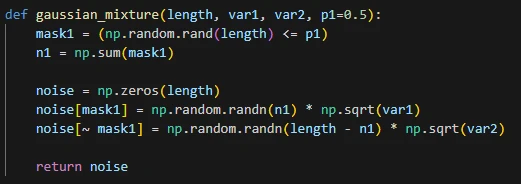
در مثال زیر با استفاده از این تابع دو سیگنال تصادفی تولید می‌کنیم. واریانس گوسی دوم را خیلی بزرگ‌تر از گوسی اول در نظر می‌گیریم. در سیگنال اول، احتمال توزیع گوسی اول (واریانس کم) را p1=0.5 و در سیگنال دوم احتمال گوسی اول را 0.8 در نظر می‌گیریم. چون در سیگنال دوم، احتمال انتخاب شدن گوسی با واریانس کمتر را 0.8 در نظر گرفته ایم (بزرگتر از احتمال p1 برای سیگنال اول هست)، انتظار می‌رود در خروجی تعداد مقادیر ضریه‌ای در سیگنال دوم کمتر از سیگنال اول باشد، چون نمونه‌های تصادفی تولید شده در سیگنال دوم با احتمال بیشتر از توزیع گوسی با واریانس کمتر تولید می‌شوند.

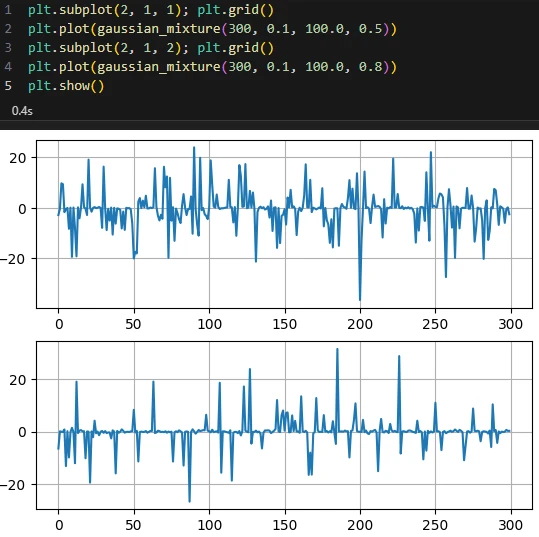
همان‌طور که انتظار داشتیم شدت ضربه‌ای بودن سیگنال اول بیشتر است.

فیلترکردن نویز گوسی ترکیبی با فیلتر میانه

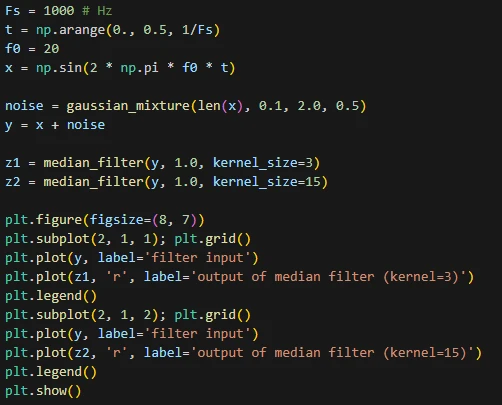
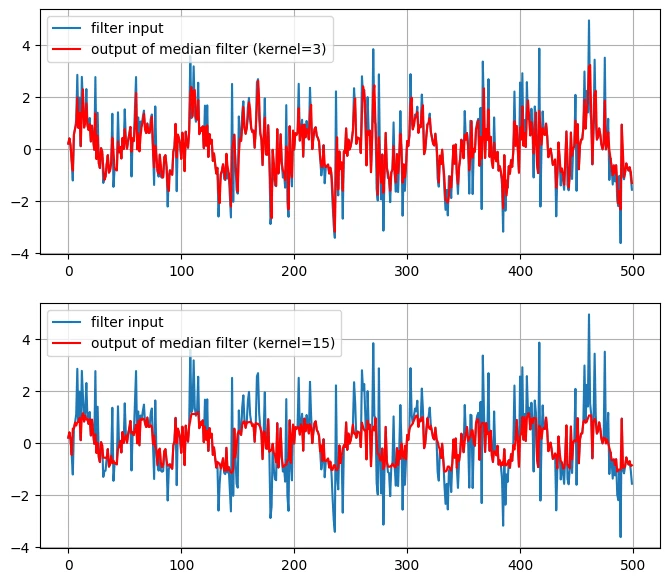
یک سیگنال سینوسی ایجاد کرده و به آن نویز گوسی ترکیبی اضافه می‌کنیم. سپس سیگنال دارای نویز را با دو فیلتر میانه با آستانه‌ی 1 و سایز کرنل‌های 3 و 15 فیلتر کرده و نمودار خروجی هر یک از فیلتر‌ها را رسم می‌کنیم.

نمودار خروجی:

فایل کدهای این آموزش را می‌توانید از لینک گیت‌هاب زیر دانلود نمایید:

https://github.com/sphrk/array_indexing_examples_in_python